Острый угол прямоугольной трапеции равен \(\displaystyle 60^{\circ}{\small.}\) Найдите боковую сторону трапеции при этом угле, если её основания равны \(\displaystyle 5\) и \(\displaystyle 9{\small.}\)
Пусть \(\displaystyle ABCD\) – прямоугольная трапеция:
Требуется найти боковую сторону \(\displaystyle CD{\small.}\) | 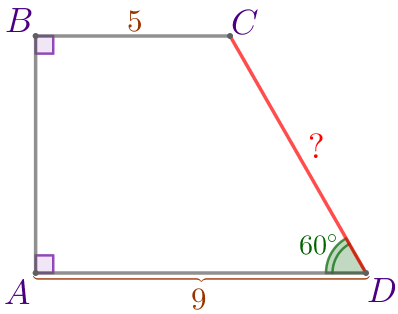 |
Из вершины \(\displaystyle C\) проведём высоту \(\displaystyle CH{\small.}\)
В четырёхугольнике \(\displaystyle ABCH\) все углы прямые, поэтому он является прямоугольником. В прямоугольнике противоположные стороны попарно равны, значит, \(\displaystyle AH=BC=5{\small.}\) | 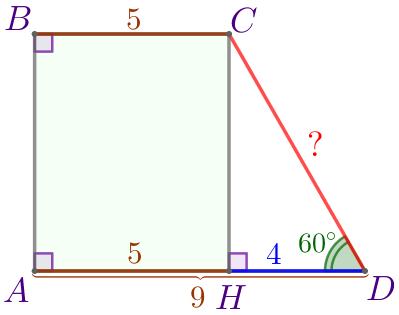 |
Тогда
\(\displaystyle HD=AD-AH=9-5=4{\small.}\)
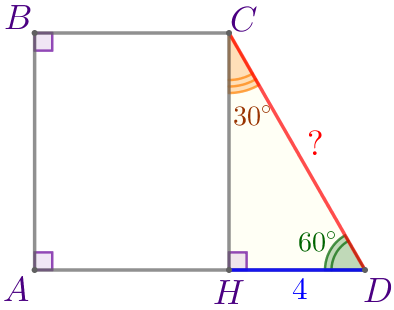
| Сумма острых углов прямоугольного треугольника равна \(\displaystyle 90^{\circ}{\small.}\) Значит, \(\displaystyle \angle HCD=90^{\circ}-\angle HDC{\small;}\) \(\displaystyle \angle HCD=90^{\circ}-60^{\circ}=30^{\circ}{\small.}\) |
Катет прямоугольного треугольника, лежащий против угла в \(\displaystyle 30^{\circ}{\small,}\) равен половине гипотенузы.
Следовательно,
\(\displaystyle CD=2 \cdot HD=2 \cdot 4=8{\small.}\)
Ответ: \(\displaystyle 8{\small.}\)