В прямоугольной трапеции основания равны \(\displaystyle 3\) и \(\displaystyle 5{\small,}\) а один из углов равен \(\displaystyle 135^{\circ}{\small.}\) Найдите меньшую боковую сторону данной трапеции.
Пусть \(\displaystyle ABCD\) – прямоугольная трапеция:
| 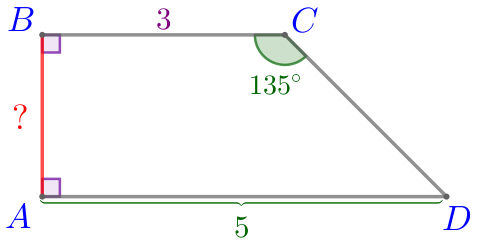 |
Требуется найти меньшую боковую сторону данной трапеции, то есть найти сторону \(\displaystyle AB{\small.}\)
\(\displaystyle \angle D=45^{\circ}{\small.}\)
Из вершины \(\displaystyle C\) проведём высоту \(\displaystyle CH{\small.}\)
В четырёхугольнике \(\displaystyle ABCH\) все углы прямые, поэтому он является прямоугольником. В прямоугольнике противоположные стороны попарно равны, значит, \(\displaystyle \color{red}{AB}=CH{\small;}\) \(\displaystyle AH=BC=3{\small.}\) | 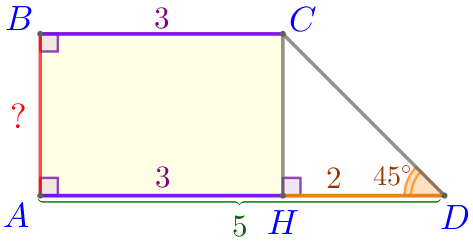 |
Тогда
\(\displaystyle HD=AD-AH=5-3=2{\small.}\)
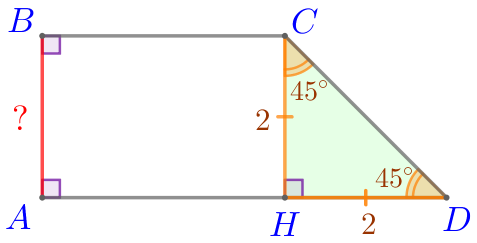
| Сумма острых углов прямоугольного треугольника равна \(\displaystyle 90^{\circ}{\small.}\) Значит, \(\displaystyle \angle HCD=90^{\circ}-\angle HDC{\small;}\) \(\displaystyle \angle HCD=90^{\circ}-45^{\circ}=45^{\circ}{\small.}\) |
Так как острые углы прямоугольного треугольника \(\displaystyle CDH\) равны, то \(\displaystyle \triangle CDH\) – равнобедренный.
То есть
\(\displaystyle CH=HD=2{\small.}\)
В результате получаем:
\(\displaystyle \color{red}{AB}=CH=2{\small.}\)
Ответ: \(\displaystyle 2{\small.}\)