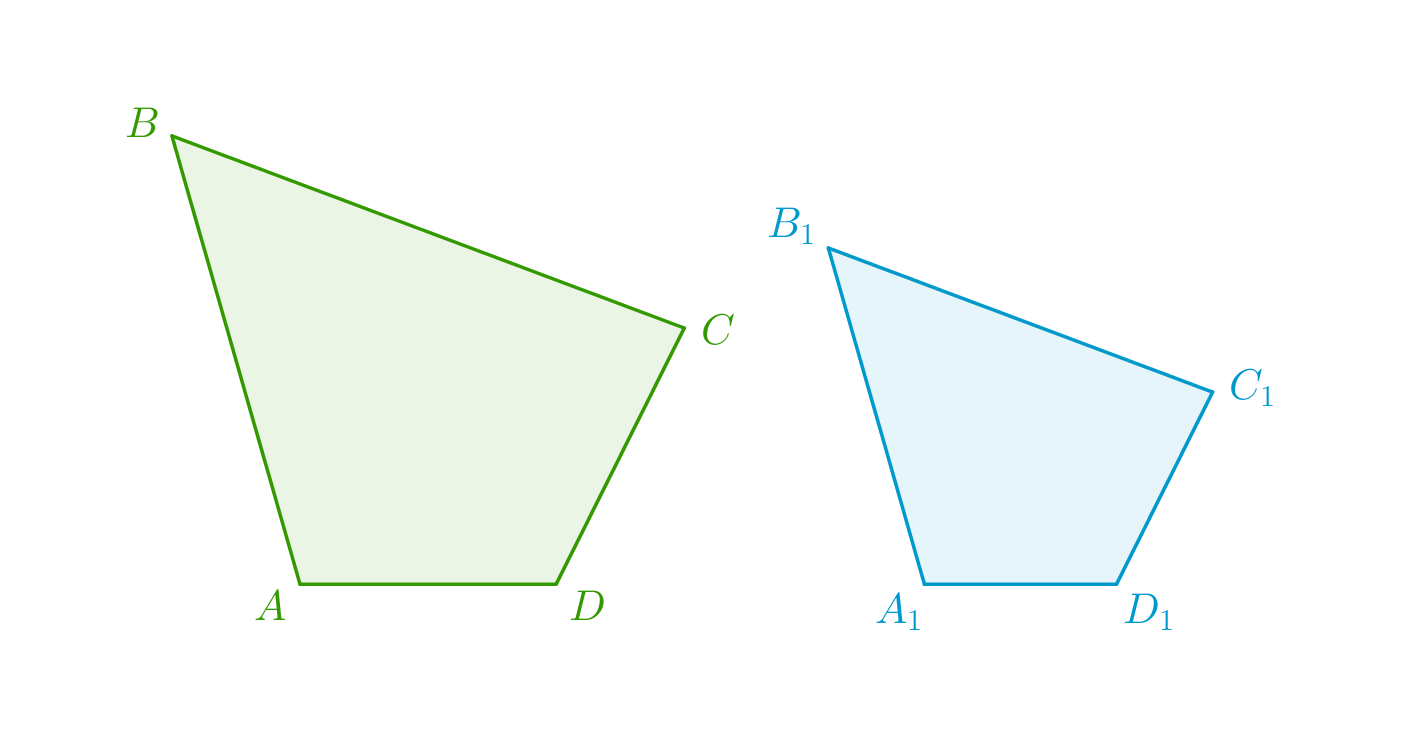
Периметр четырехугольника \(\displaystyle ABCD\) относится к периметру подобного ему четырехугольника \(\displaystyle A_1B_1C_1D_1\) как \(\displaystyle 4:3\small.\) Длина стороны \(\displaystyle BC=17\)см, а длина \(\displaystyle B_1C_1\) на \(\displaystyle 6{,}75\)см больше длины стороны \(\displaystyle A_1D_1\small.\) Найдите длину стороны \(\displaystyle AD\small.\)
\(\displaystyle AD=\) см.
Отношение периметров подобных многоугольников
Отношение периметров подобных многоугольников равно коэффициенту подобия этих многоугольников.
Тогда для четырехугольников из условия коэффициент подобия равен:
\(\displaystyle k=\frac{P_{ABCD}}{P_{A_1B_1C_1D_1}}=\frac{4}{3}\small.\)
Таким образом, для сходственных сторон многоугольников выполняется:
\(\displaystyle \frac{BC}{B_1C_1}=k=\frac{4}{3}\small.\)
Подставляем значение \(\displaystyle BC=17\)см из условия и получаем:
\(\displaystyle B_1C_1=\frac{BC}{k}=\frac{17}{\phantom{11}\dfrac{4}{3}\phantom{11}}=12{,}75\)см.
Зная \(\displaystyle B_1C_1\small,\) вычислим \(\displaystyle A_1D_1\small{:}\)
\(\displaystyle A_1D_1=B_1C_1-6{,}75=12{,}75-6{,}75=6\)см.
Учитывая, что \(\displaystyle \frac{AD}{A_1D_1}=k=\frac{4}{3}\small,\) получаем:
\(\displaystyle AD=A_1D_1 \cdot k= 6\cdot \frac{4}{3}=8\)см.
Ответ: \(\displaystyle 8\)см.