Пользуясь фактом, что все окружности подобны, определите, во сколько раз площадь окружности с центром \(\displaystyle O_1\) больше площади окружности с центром \(\displaystyle O_2\small?\)
Отношение площадей подобных фигур
Отношение площадей двух подобных фигур равно квадрату коэффициента подобия этих фигур.
Коэффициент подобия окружностей можно вычислить как отношение длин радиусов этих окружностей.
Радиус окружности с центром в точке \(\displaystyle O_1\) равен \(\displaystyle 5\small,\) а радиус окружности с центром в точке \(\displaystyle O_2\) равен \(\displaystyle 3\small,\) тогда коэффициент подобия этих окружностей равен: \(\displaystyle k=\frac{R_1}{R_2}=\frac{5}{3}\small.\) | 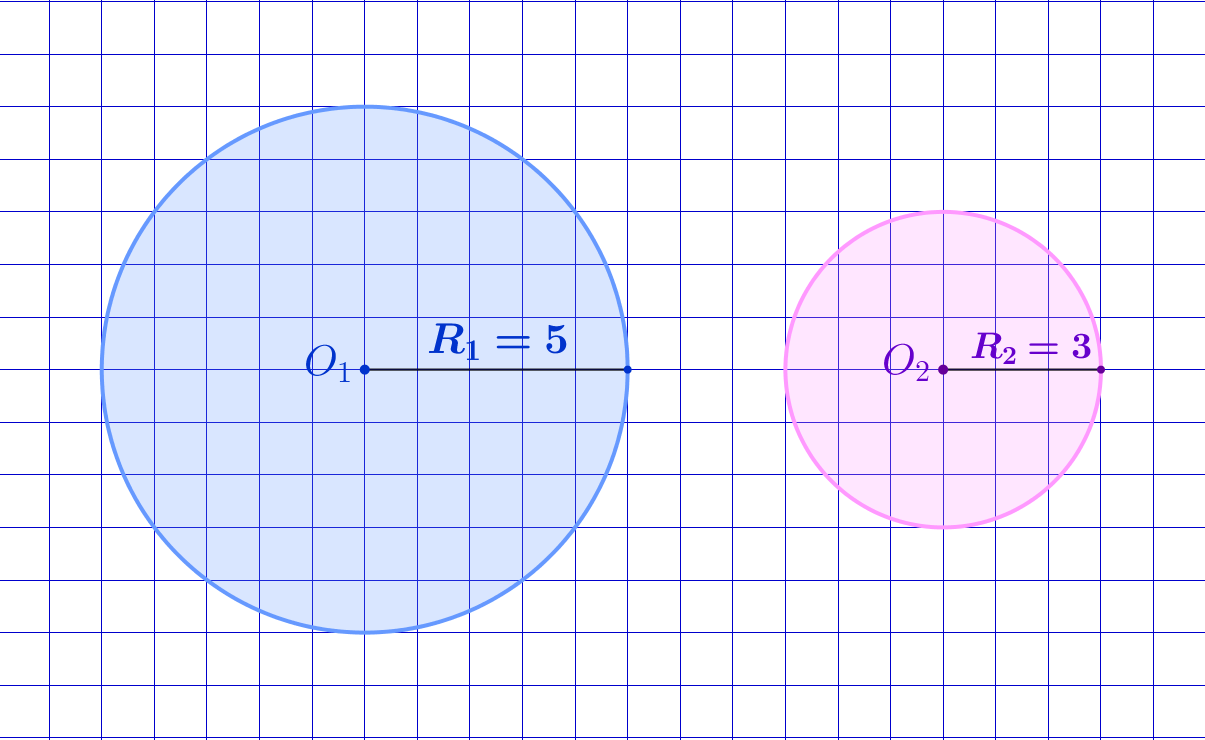 |
Таким образом, отношение площадей:
\(\displaystyle \frac{S_1}{S_2}=k^2=\left( \frac{5}{3} \right) ^2=\frac{25}{9}\small.\)