На каких рисунках изображены подобные фигуры?
| Рисунок 1 | Рисунок 2 |
 |  |
| Рисунок 3 | Рисунок 4 |
 |  |
Подобные многоугольники
Два многоугольника называются подобными, если их сходственные стороны пропорциональны, а соответственные углы равны.
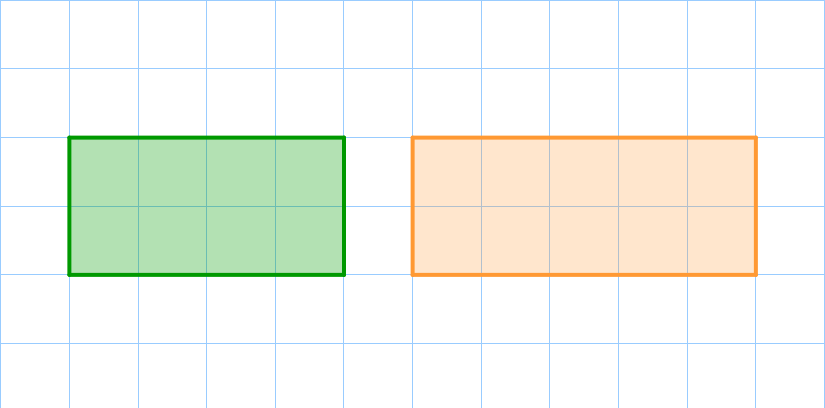
Прямоугольники, изображенные на рисунке, не являются подобными.
Несмотря на то, что углы этих прямоугольников равны, их стороны не пропорциональны.
Отношение меньших сторон и отношение больших сторон отличаются: \(\displaystyle \frac{2}{2}\cancel= \frac{4}{5}\small.\) | 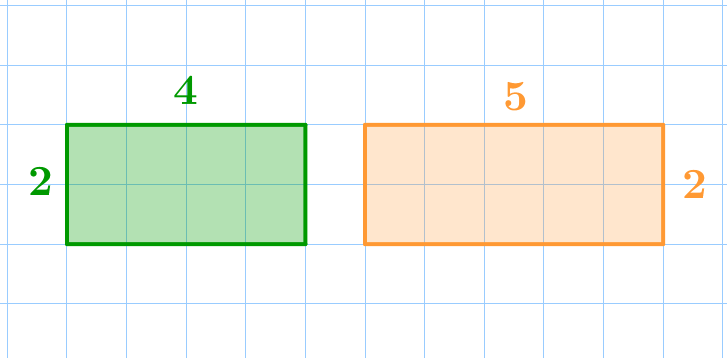 |
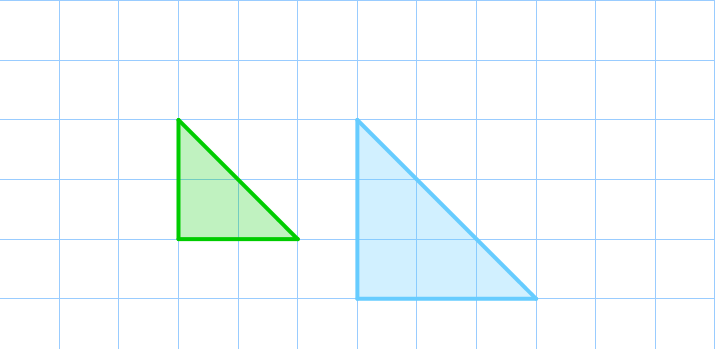
Прямоугольные треугольники, изображенные на рисунке, подобны.
Эти треугольники равнобедренные, значит, их углы равны \(\displaystyle 45^\circ\small,\) \(\displaystyle 45^\circ\) и \(\displaystyle 90^\circ\small.\) При этом отношения их сходственных сторон равны:
Отношения катетов и гипотенуз равны: \(\displaystyle \frac{2}{3}=\frac{2}{3}=\frac{2\sqrt2}{3\sqrt2}\small.\) | 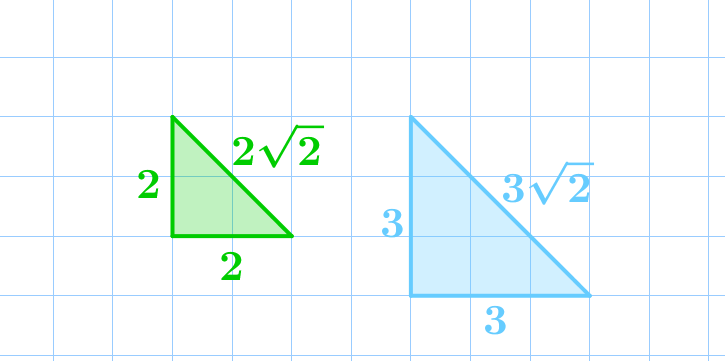 |
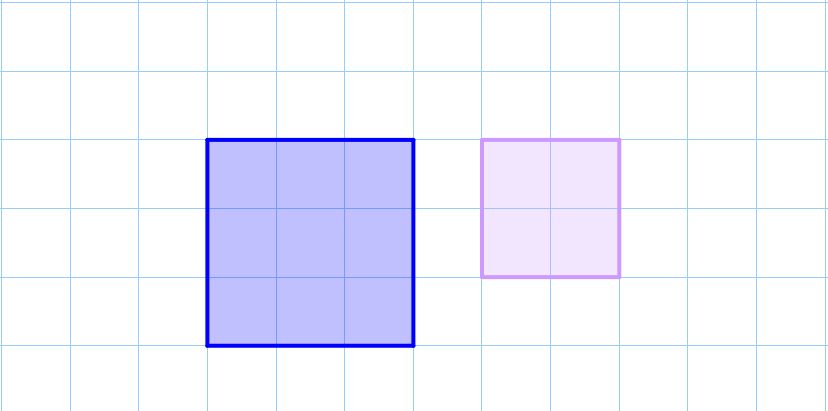
Любые два квадрата подобны.
Так как у квадрата все четыре угла прямые и все стороны равны, то любые два квадрата подобны. При этом коэффициент подобия равен отношению длины стороны одного квадрата к длине стороны другого.
Коэффициент подобия равен: \(\displaystyle k=\frac{3}{2}\small.\) | 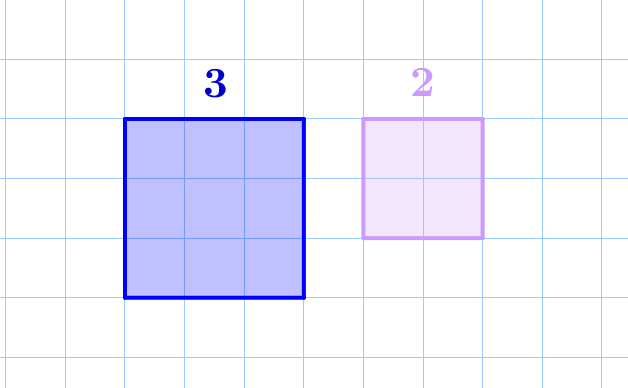 |
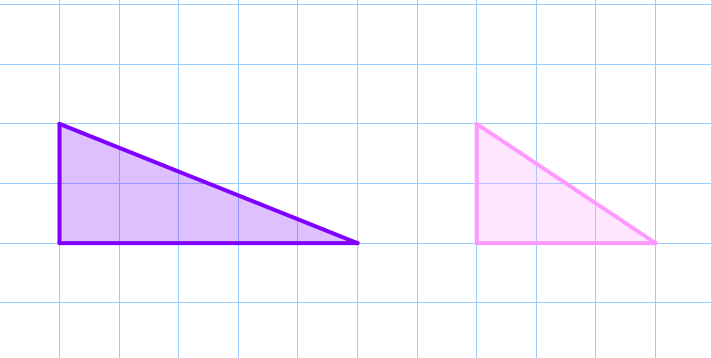
Прямоугольные треугольники, изображенные на рисунке, не являются подобными.
Не смотря на то, что углы этих прямоугольников равны, их стороны не пропорциональны.
Отношение больших и меньших катетов, а также отношение гипотенуз отличаются: \(\displaystyle \frac{2}{2}\cancel= \frac{5}{3}\cancel=\frac{\sqrt{29}}{\sqrt{13}}\small.\) | 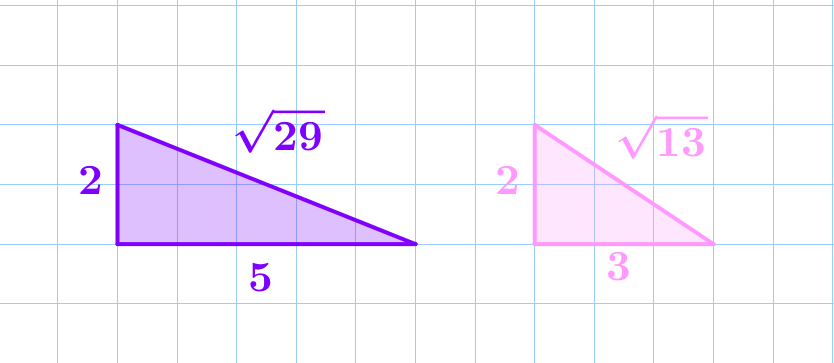 |