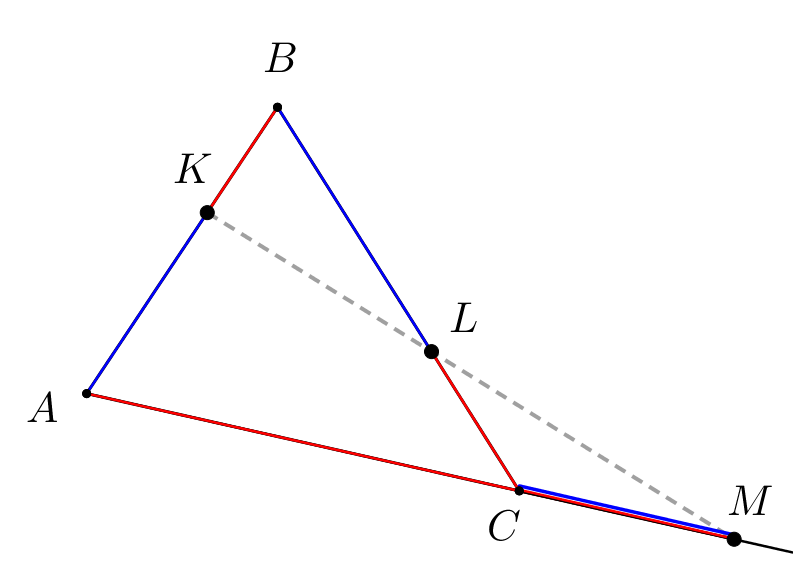
Вписанная окружность треугольника \(\displaystyle ABC\) касается его сторон \(\displaystyle AB,\,BC\) и \(\displaystyle AC\) в точках \(\displaystyle K,\,L\) и \(\displaystyle M\) соответственно. Прямая \(\displaystyle KL\) пересекает продолжение стороны \(\displaystyle AC\) в точке \(\displaystyle N{\small.}\)
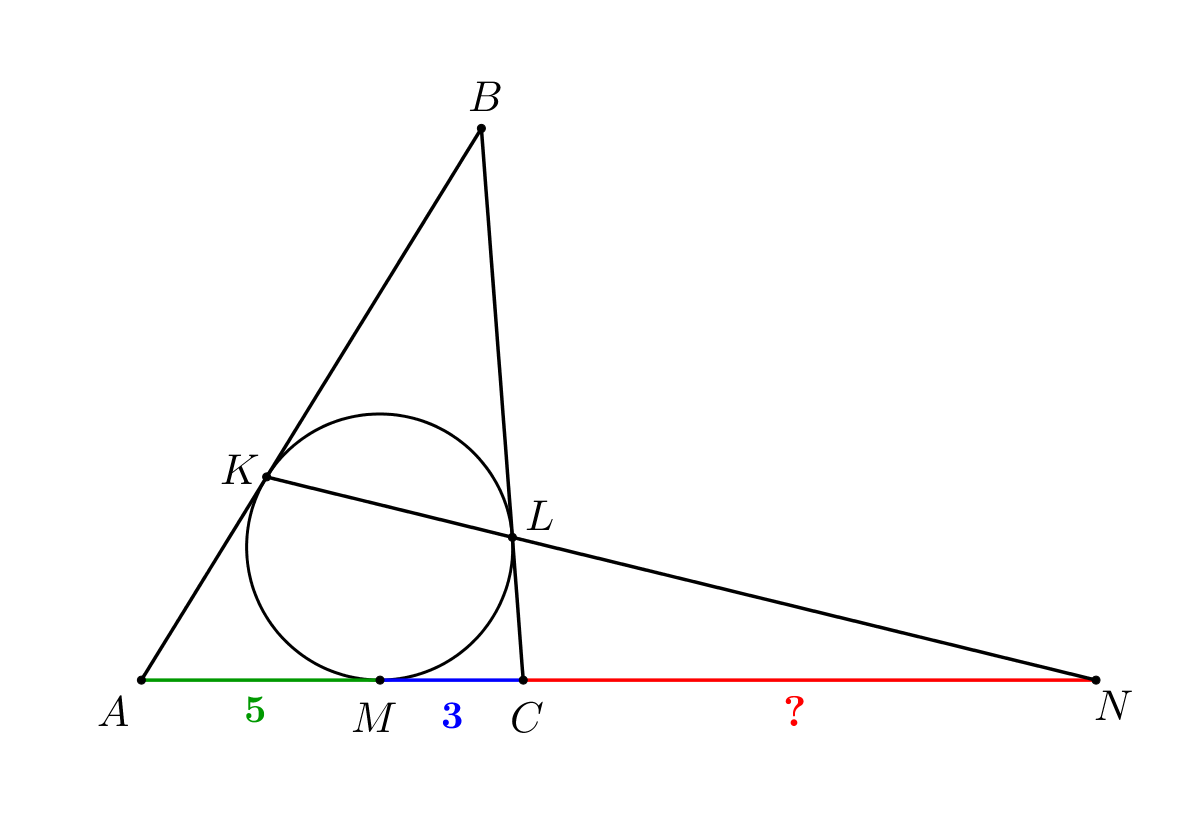
Найдите \(\displaystyle CN\small,\) если \(\displaystyle AM=5\) и \(\displaystyle CM=3\small.\)
Чтобы решить задачу:
- напишем теорему Менелая для треугольника \(\displaystyle ABC\) и прямой \(\displaystyle KL\small,\)
- воспользуемся тем, что отрезки касательных, проведенных из одной точки, равны, и найдем \(\displaystyle CN\small.\)
1. Точки \(\displaystyle K,\,L\) и \(\displaystyle N\) лежат на одной прямой. Тогда по теореме Менелая для треугольника \(\displaystyle ABC\) и прямой \(\displaystyle KL\small,\) получаем: \(\displaystyle \frac{\color{blue}{AK}}{\color{red}{KB}}\cdot\frac{\color{blue}{BL}}{\color{red}{LC}}\cdot\frac{\color{blue}{CN}}{\color{red}{NA}}=1\small.\) | 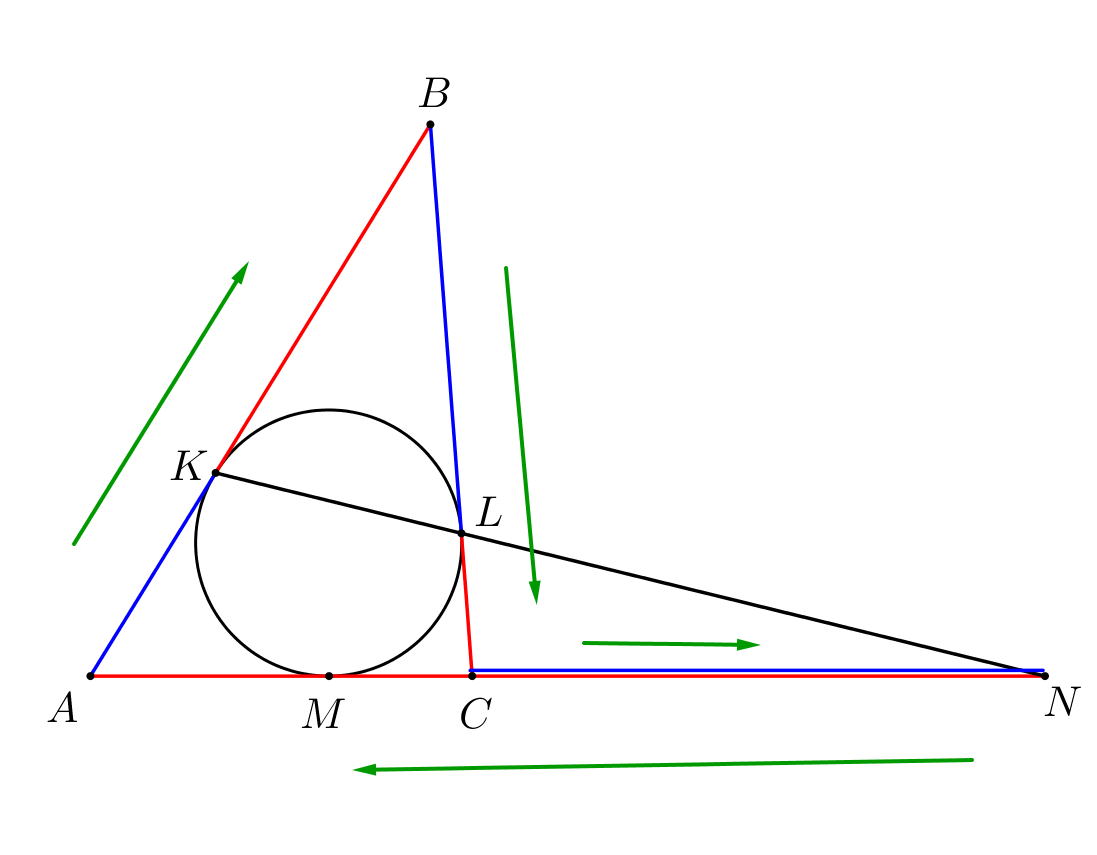 |
2. Поскольку отрезки касательных, проведенных из одной точки, равны, то
Обозначим \(\displaystyle CN\) за \(\displaystyle \color{red}x\small,\) тогда \(\displaystyle AN=3+5+x{\small.}\) | 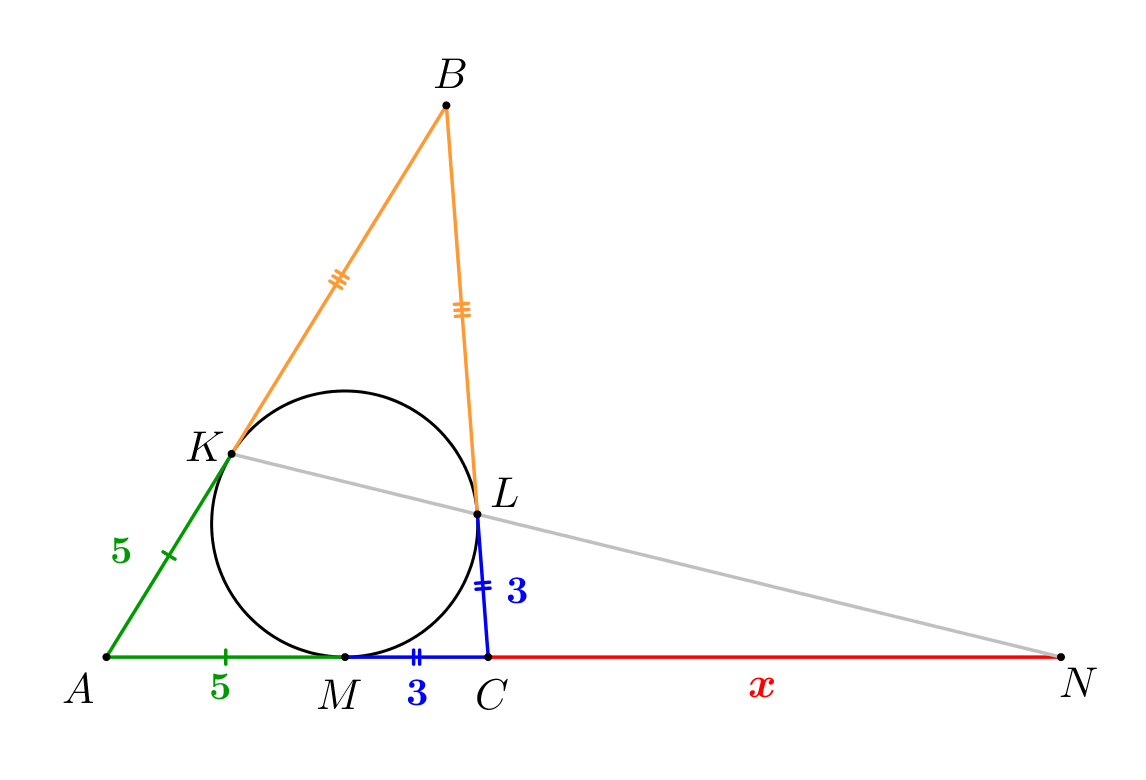 |
Подставим полученные значения в равенство из теоремы Менелая и сократим равные множители \(\displaystyle BK\) и \(\displaystyle BL\) в числителе и знаменателе:
\(\displaystyle \frac{AK}{\cancel{BK}}\cdot\frac{\cancel{BL}}{LC}\cdot\frac{CN}{NA}=\frac{5\cdot x}{3\cdot(8+x)}=1\small.\)
\(\displaystyle x=12\)
То есть \(\displaystyle CN=x=12\small.\)
Ответ: \(\displaystyle CN=12\small.\)