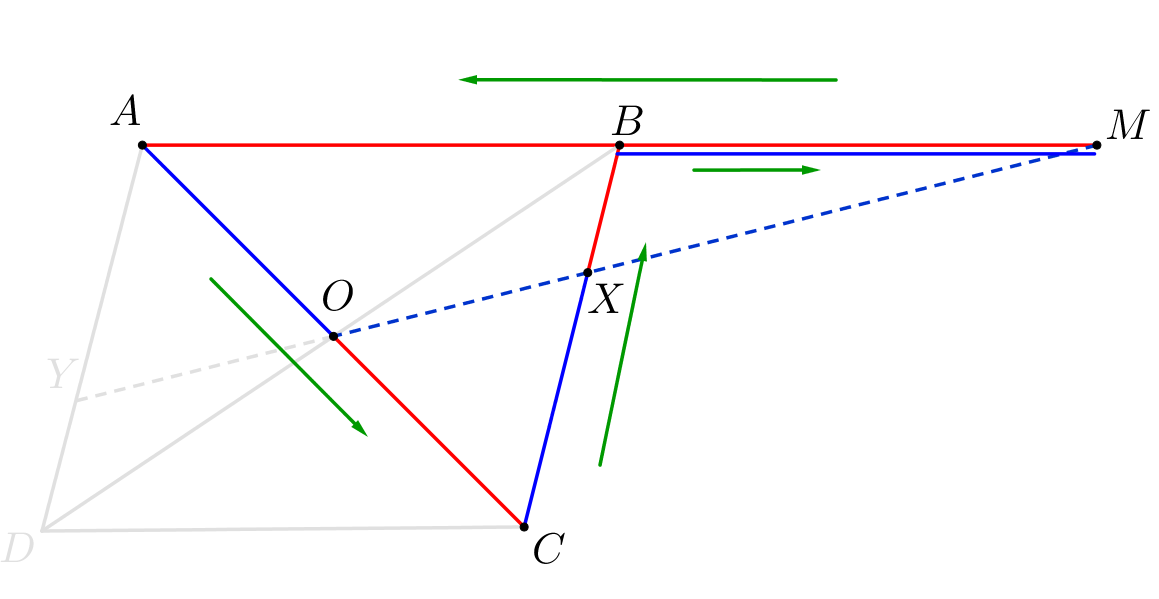
На продолжении стороны \(\displaystyle AB\) параллелограмма \(\displaystyle ABCD\) взяли точку \(\displaystyle M\) так, что \(\displaystyle BM = AB\small.\) Через точку \(\displaystyle M\) и центр параллелограмма провели прямую. В каком отношении эта прямая делит стороны параллелограмма?
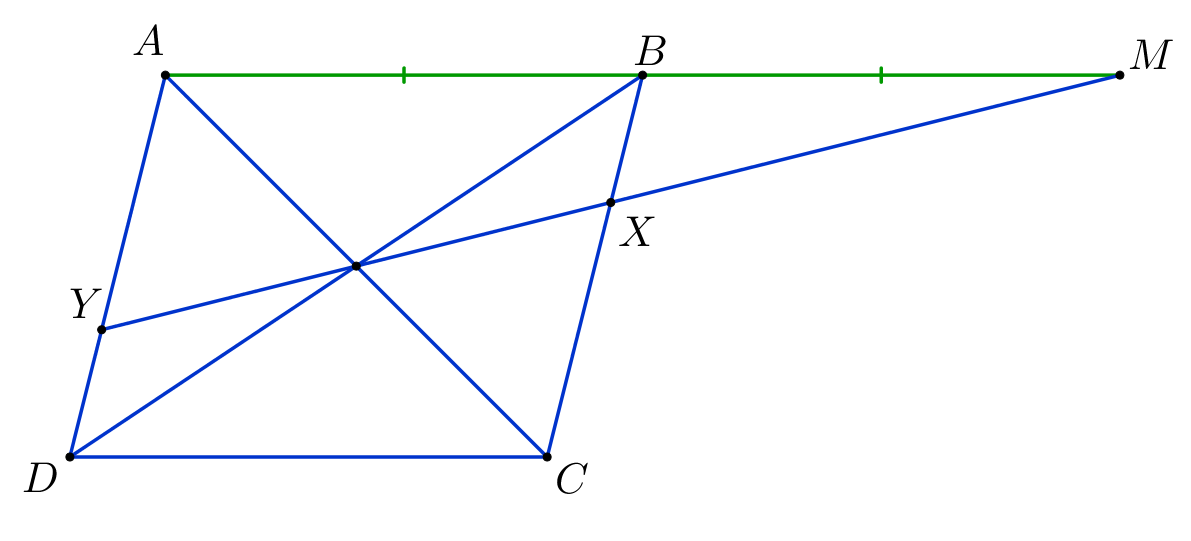
(Центром параллелограмма называют точку пересечения его диагоналей.)
Обозначим точку пересечения диагоналей параллелограмма – \(\displaystyle O\small.\)
\(\displaystyle \frac{AY}{DY}=2\small.\)
Точки \(\displaystyle Y,\,O\) и \(\displaystyle M\) лежат на одной прямой. Тогда по теореме Менелая для треугольника \(\displaystyle BDA\) и прямой \(\displaystyle YO\) получаем: \(\displaystyle \frac{\color{blue}{AY}}{\color{red}{YD}}\cdot\frac{\color{blue}{DO}}{\color{red}{OB}}\cdot\frac{\color{blue}{BM}}{\color{red}{MA}}=1\small.\) | 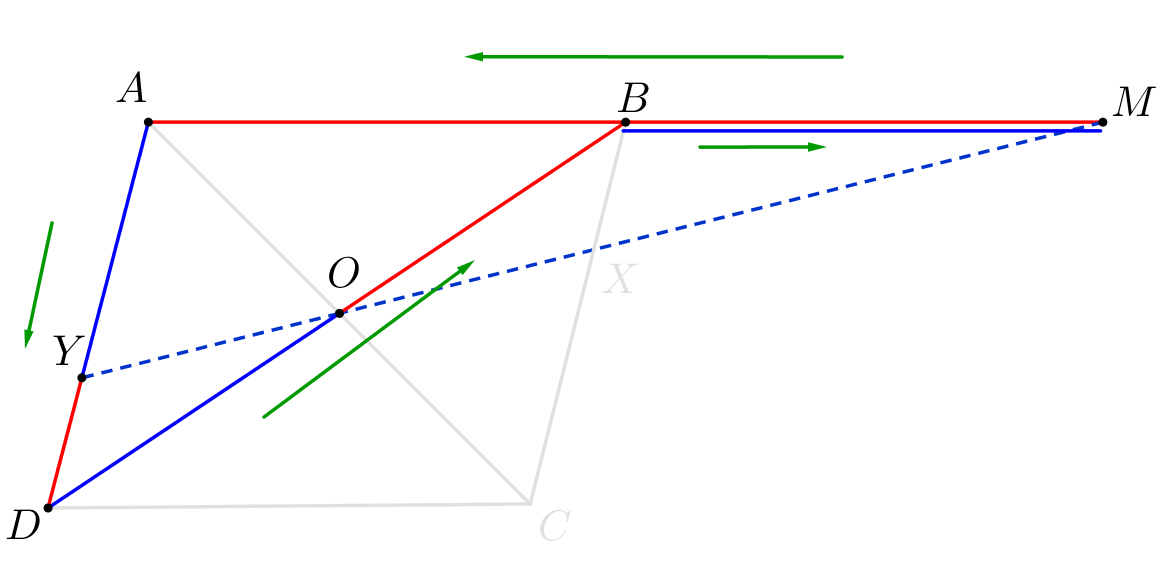 |
Найдем два отношения из трех:
- диагонали параллелограмма делятся точкой пересечения пополам, значит, \(\displaystyle \frac{DO}{BO}=1{\small:}\)
- поскольку \(\displaystyle AB=BM\small,\) то \(\displaystyle \frac{BM}{AM}=\frac{BM}{AB+BM}=\frac{BM}{BM+BM}=\frac{1}{2}\small.\)
Подставляя, получаем:
\(\displaystyle \frac{AY}{DY}\cdot1\cdot\frac{1}{2}=1\small.\)
То есть
\(\displaystyle \frac{AY}{DY}=2\small.\)
\(\displaystyle \frac{BX}{CX}=\frac{1}{2}\small.\)