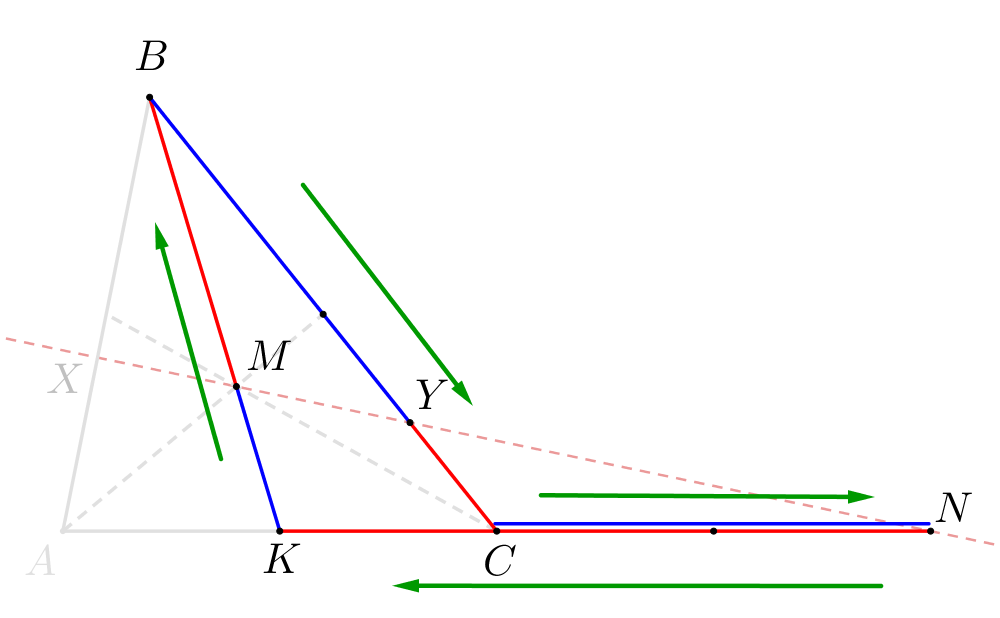
Медианы треугольника \(\displaystyle ABC\) пересекаются в точке \(\displaystyle M\small.\) На прямой \(\displaystyle AC\) взяли точку \(\displaystyle N\) так, что точка \(\displaystyle C\) – середина отрезка \(\displaystyle AN\small.\) В каком отношении прямая \(\displaystyle MN\) делит стороны \(\displaystyle AB\) и \(\displaystyle BC\) треугольника?
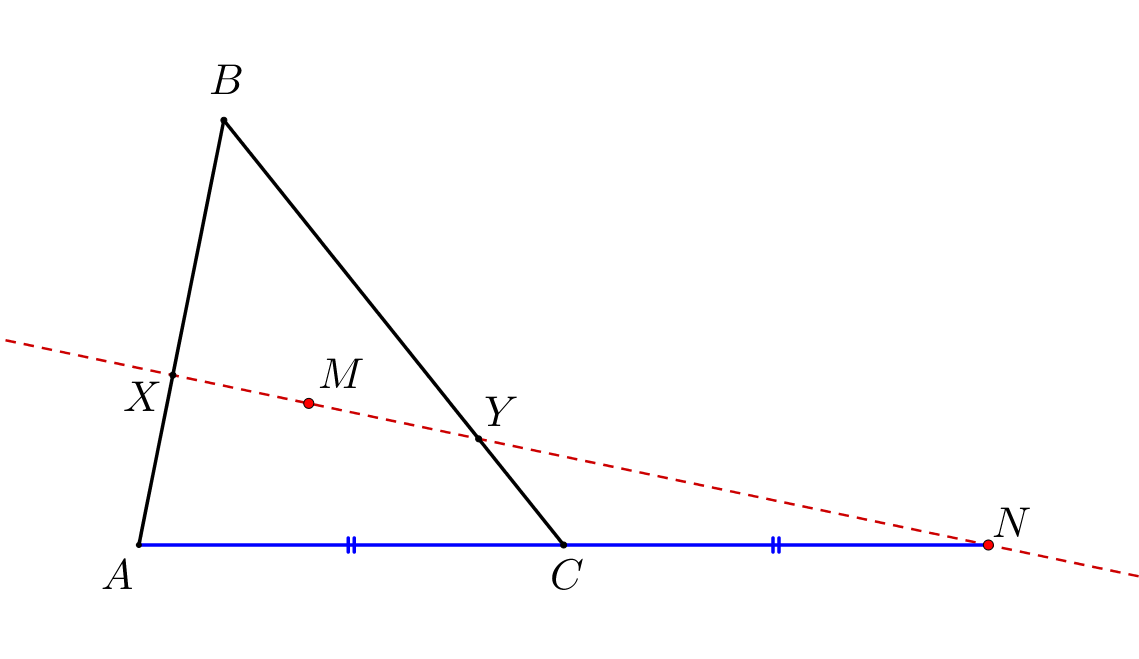
Точка \(\displaystyle K\) – середина стороны \(\displaystyle AC\small,\) получаем: \(\displaystyle AK=CK=\frac{AC}{2}=\frac{CN}{2}\small.\) Также известно, что медиана делится точкой пересечения медиан в отношении два к одному. То есть \(\displaystyle \frac{BM}{KM}=\frac{2}{1}\small.\) | 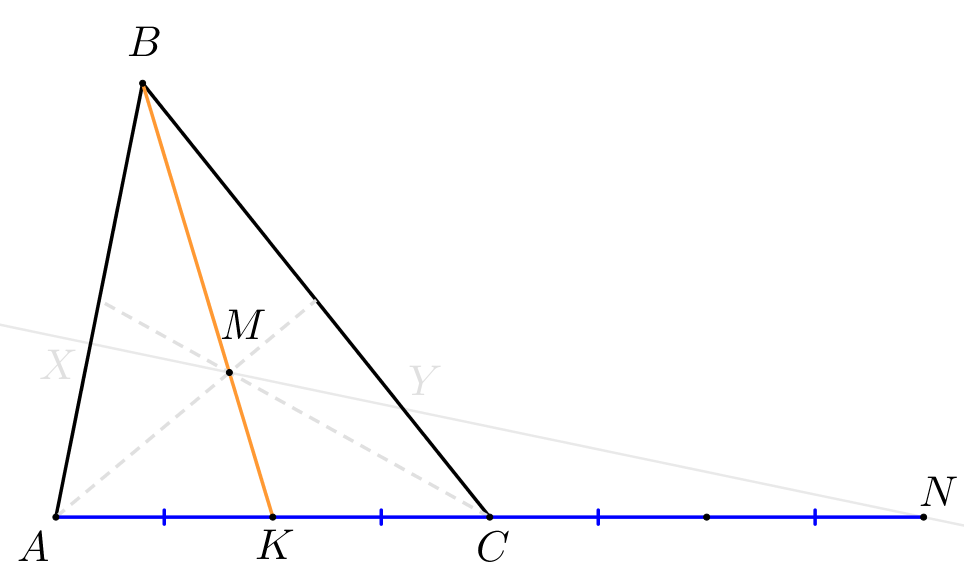 |
Теперь чтобы решить задачу:
- применяя теорему Менелая для треугольника \(\displaystyle ABK\) и прямой \(\displaystyle MN\small,\) найдем \(\displaystyle AX:BX{\small;}\)
- применяя теорему Менелая для треугольника \(\displaystyle CBK\) и прямой \(\displaystyle MN\small,\) найдем \(\displaystyle BY:CY\small.\)
\(\displaystyle \frac{AX}{BX}=\frac{2}{3}\small.\)
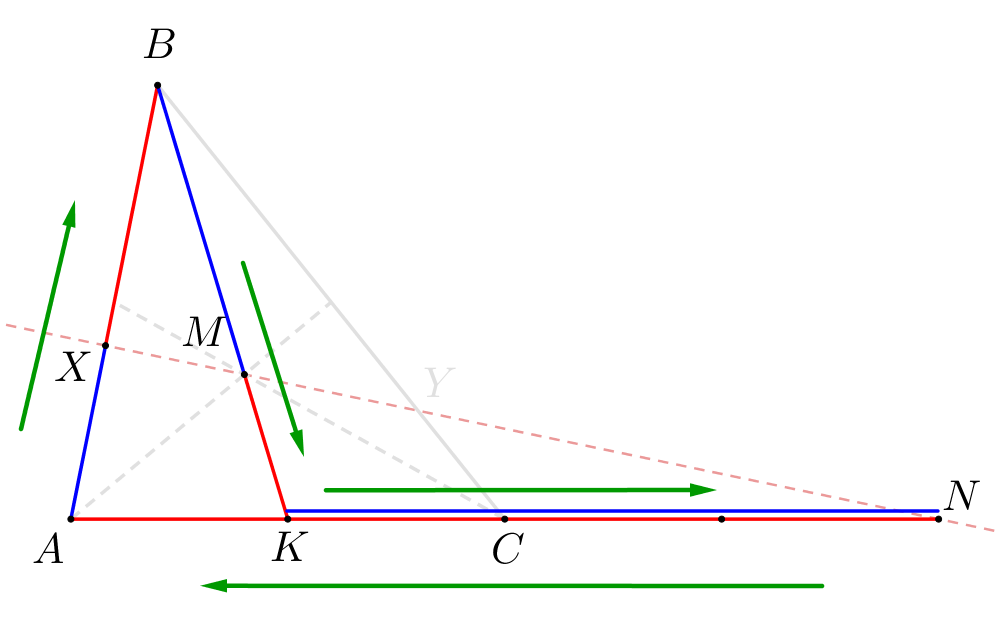
Точки \(\displaystyle X,\,M\) и \(\displaystyle N\) лежат на одной прямой. Значит, по теореме Менелая для треугольника \(\displaystyle ABK\) и прямой \(\displaystyle MN\small,\) получаем: \(\displaystyle \frac{\color{blue}{AX}}{\color{red}{XB}}\cdot\frac{\color{blue}{BM}}{\color{red}{MK}}\cdot\frac{\color{blue}{KN}}{\color{red}{NA}}=1\small.\)
|  |
Подставим известные отношения:
- \(\displaystyle \frac{BM}{KM}=\frac{2}{1}\small,\)
- \(\displaystyle \frac{KN}{AN}=\frac{KC+CN}{AC+CN}=\frac{\frac{CN}{2}+CN}{2CN}=\frac{3}{4}\small.\)
Получаем:
\(\displaystyle \frac{AX}{BX}\cdot\frac{2}{1}\cdot\frac{3}{4}=1\small,\)
\(\displaystyle \frac{AX}{BX}=\frac{2}{3}\small.\)
\(\displaystyle \frac{BY}{CY}=3\small.\)
Ответ: \(\displaystyle \frac{AX}{BX}=\frac{2}{3}\) и \(\displaystyle \frac{BY}{CY}=3\small.\)