Основания равнобедренной трапеции равны \(\displaystyle 15\) и \(\displaystyle 9\small,\) один из углов равен \(\displaystyle 45^\circ\small.\) Найдите высоту трапеции.
Пусть \(\displaystyle ABCD\) – равнобедренная трапеция:
Требуется найти высоту трапеции. | 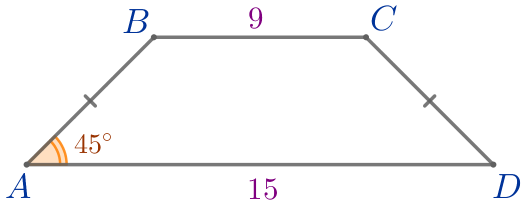 |
\(\displaystyle \angle CDA=\angle BAD=45^{\circ}{\small.}\)
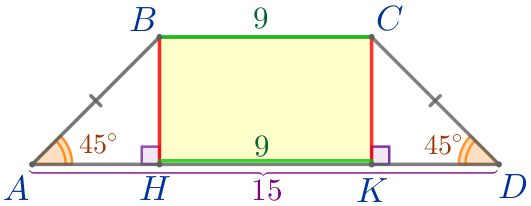
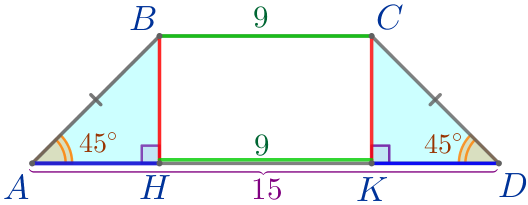
Выполним дополнительное построение. Из вершин \(\displaystyle B\) и \(\displaystyle C\) трапеции \(\displaystyle ABCD\) проведём высоты \(\displaystyle BH\) и \(\displaystyle CK{\small.}\) | 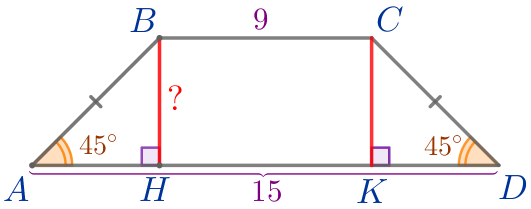 |
\(\displaystyle HK=BC=9{\small.}\)
\(\displaystyle AH=KD=3{\small.}\)
Найдём высоту \(\displaystyle BH\) из прямоугольного треугольника \(\displaystyle ABH{\small:}\)
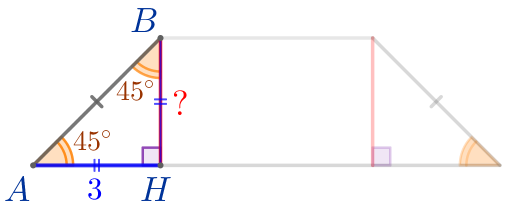 | Сумма острых углов прямоугольного треугольника равна \(\displaystyle 90^{\circ}{\small.}\) Значит, \(\displaystyle \angle ABH=90^{\circ}-\angle BAH{\small;}\) \(\displaystyle \angle ABH=90^{\circ}-45^{\circ}=45^{\circ}{\small.}\) |
Так как \(\displaystyle \angle ABH=\angle BAH{\small,}\) то \(\displaystyle \triangle ABH\) – равнобедренный. Следовательно, \(\displaystyle BH=AH=3{\small.}\) | |
То есть высота трапеции равна \(\displaystyle 3{\small.}\)
Ответ: \(\displaystyle 3{\small.}\)