В равнобедренной трапеции высота равна \(\displaystyle 3{\small,}\) бóльшее основание равно \(\displaystyle 8{\small,}\) а угол при основании равен \(\displaystyle 45^{\circ}{\small.}\) Найдите меньшее основание трапеции.
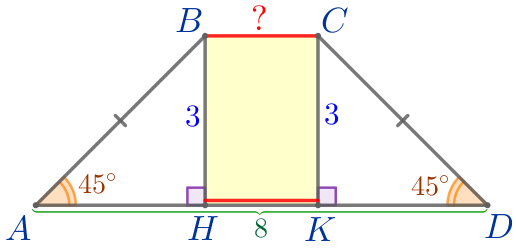
Пусть \(\displaystyle ABCD\) – равнобедренная трапеция:
Требуется найти длину основания \(\displaystyle BC{\small.}\) | 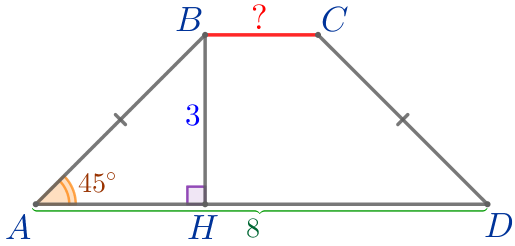 |
\(\displaystyle \angle CDA=\angle BAD=45^{\circ}{\small.}\)
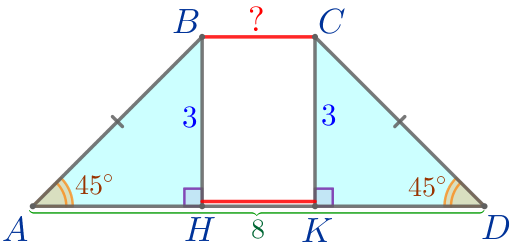
Выполним дополнительное построение. Из вершины \(\displaystyle C\) проведём высоту \(\displaystyle CK{\small.}\) Высоты трапеции равны: \(\displaystyle CK=BH=3{\small.}\) | 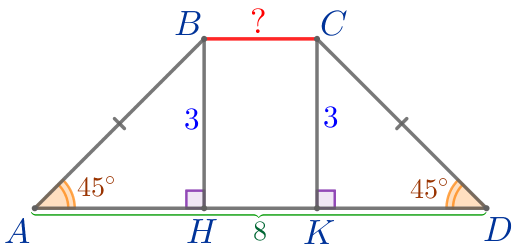 |
\(\displaystyle \color{red}{BC}=HK{\small.}\)
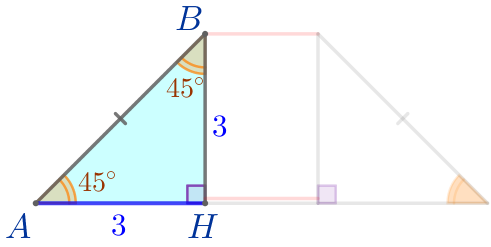
\(\displaystyle AH=KD=3{\small.}\)
Найдём длину отрезка \(\displaystyle HK{\small.}\)
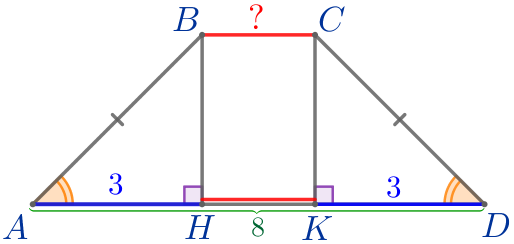 | Точки \(\displaystyle H\) и \(\displaystyle K\) лежат на основании \(\displaystyle AD{\small,}\) значит, \(\displaystyle AD=AH+HK+KD{\small.}\) Тогда \(\displaystyle HK=AD-(AH+KD){\small;}\) \(\displaystyle HK=8-(3+3)=8-6=2{\small.}\) |
Следовательно,
\(\displaystyle \color{red}{BC}=2{\small.}\)
Ответ: \(\displaystyle 2{\small.}\)