Теория: Разные задачи (короткая версия)

Задание

В равнобедренной трапеции бóльшее основание равно \(\displaystyle 25{\small,}\) боковая сторона равна \(\displaystyle 10{\small,}\) угол между ними \(\displaystyle 60^{\circ}{\small.}\) Найдите меньшее основание.

Решение

Пусть \(\displaystyle ABCD\) – равнобедренная трапеция:

\(\displaystyle AB=CD=10\) – боковые стороны;
\(\displaystyle AD=25\) – бóльшее основание;
\(\displaystyle \angle BAD=60^{\circ}{\small.}\)

Требуется найти длину основания \(\displaystyle BC{\small.}\)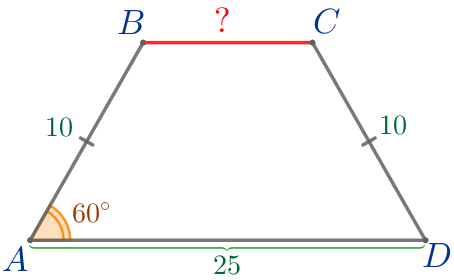

Поскольку трапеция \(\displaystyle ABCD\) равнобедренная, то

\(\displaystyle \angle CDA=\angle BAD=60^{\circ}{\small.}\)

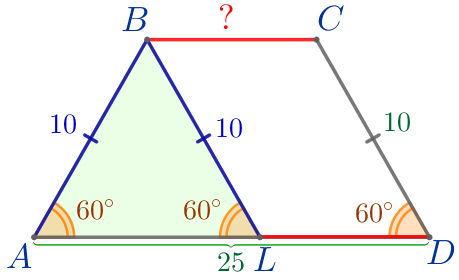
Выполним дополнительное построение.

На стороне \(\displaystyle AD\) отметим точку \(\displaystyle L\) так, что

\(\displaystyle BL \parallel CD{\small.}\)

Проведём отрезок \(\displaystyle BL{\small.}\)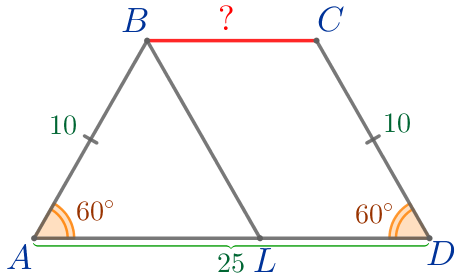

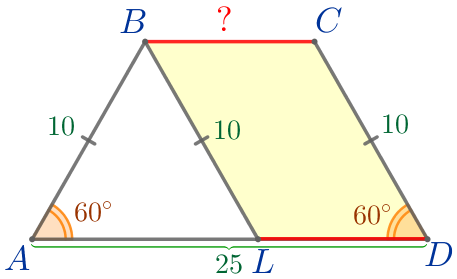Рассмотрим четырёхугольник \(\displaystyle BCDL{\small.}\)

\(\displaystyle BC \parallel LD\) – так как лежат на основаниях трапеции;
\(\displaystyle BL \parallel CD\) – по построению.

Следовательно, по определению

\(\displaystyle BCDL\) – параллелограмм.

В параллелограмме противоположные стороны попарно равны, значит,

\(\displaystyle \color{red}{BC}=LD{\small;}\)

\(\displaystyle BL=CD=10{\small.}\)

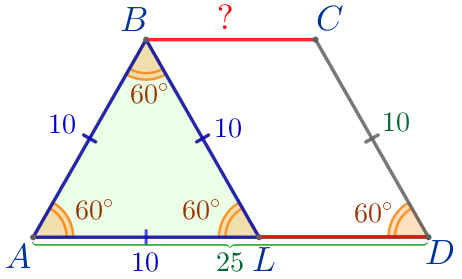
\(\displaystyle AL=10{\small.}\)

Так как точка \(\displaystyle L\) лежит на основании \(\displaystyle AD{\small,}\) то

\(\displaystyle LD=AD-AL{\small.}\)

Подставим \(\displaystyle AD=25{\small,}\) \(\displaystyle AL=10{\small:}\)

\(\displaystyle LD=25-10=15{\small.}\)

Значит,

\(\displaystyle \color{red}{BC}=15{\small.}\)

Меньшее основание трапеции равно \(\displaystyle 15{\small.}\)

Ответ: \(\displaystyle 15{\small.}\)