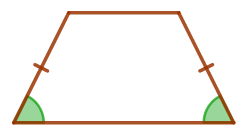
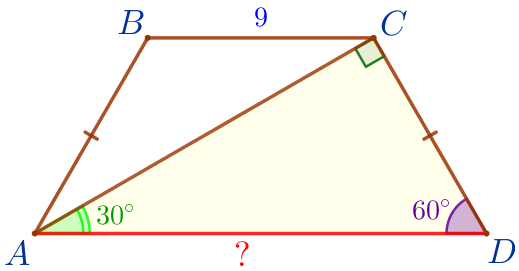
В равнобедренной трапеции \(\displaystyle ABCD\) с бóльшим основанием \(\displaystyle AD\) диагональ \(\displaystyle AC\) перпендикулярна к боковой стороне \(\displaystyle CD{\small.}\) Найдите \(\displaystyle AD{\small,}\) если \(\displaystyle BC=9\, \footnotesize см{\small,}\) а \(\displaystyle \angle D=60^{\circ}{\small.}\)
\(\displaystyle AD=\) \(\displaystyle \footnotesize см{\small.}\)
\(\displaystyle ABCD\) – равнобедренная трапеция:
Требуется найти длину основания \(\displaystyle \color{red}{AD}{\small.}\) | 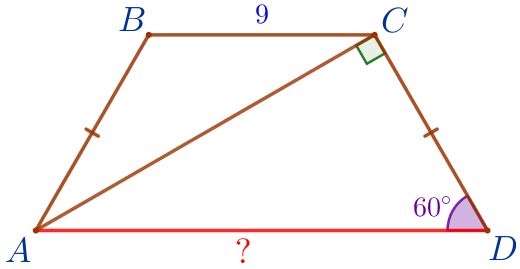 |
\(\displaystyle \angle BAD=\angle CDA=60^{\circ}{\small.}\)
\(\displaystyle \angle CAD=30^{\circ}{\small;}\)
\(\displaystyle \color{red}{AD}=2\cdot CD{\small.}\)
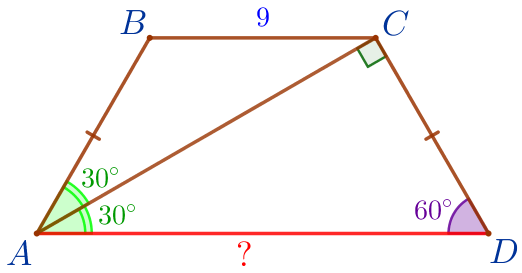
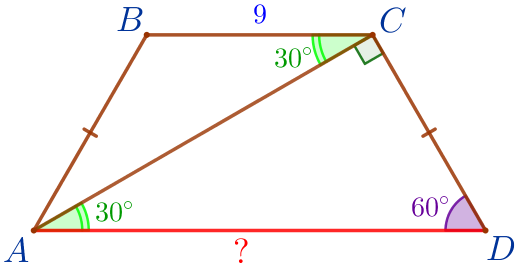
\(\displaystyle \angle BAC=\angle BCA=30^{\circ}{\small.}\)
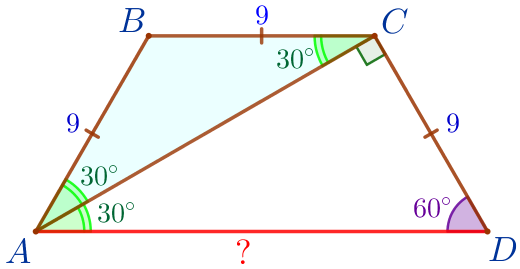 | В треугольнике \(\displaystyle ABC\) два угла равны, следовательно, \(\displaystyle \triangle ABC\) – равнобедренный: \(\displaystyle AB=BC=9\, \footnotesize см{\small.}\) |
Поскольку боковые стороны равнобедренной трапеции равны, то \(\displaystyle CD=AB=9\, \footnotesize см{\small.}\) | |
В результате получаем
\(\displaystyle \color{red}{AD}=2\cdot CD=2 \cdot 9=18\, \footnotesize см{\small.}\)
Бóльшее основание трапеции равно \(\displaystyle 18\, \footnotesize см{\small.}\)
Ответ: \(\displaystyle 18\, \footnotesize см{\small.}\)