Прямые \(\displaystyle AB{\small ,\;}MN\) и \(\displaystyle PQ\) пересекаются в точке \(\displaystyle O{\small .}\)
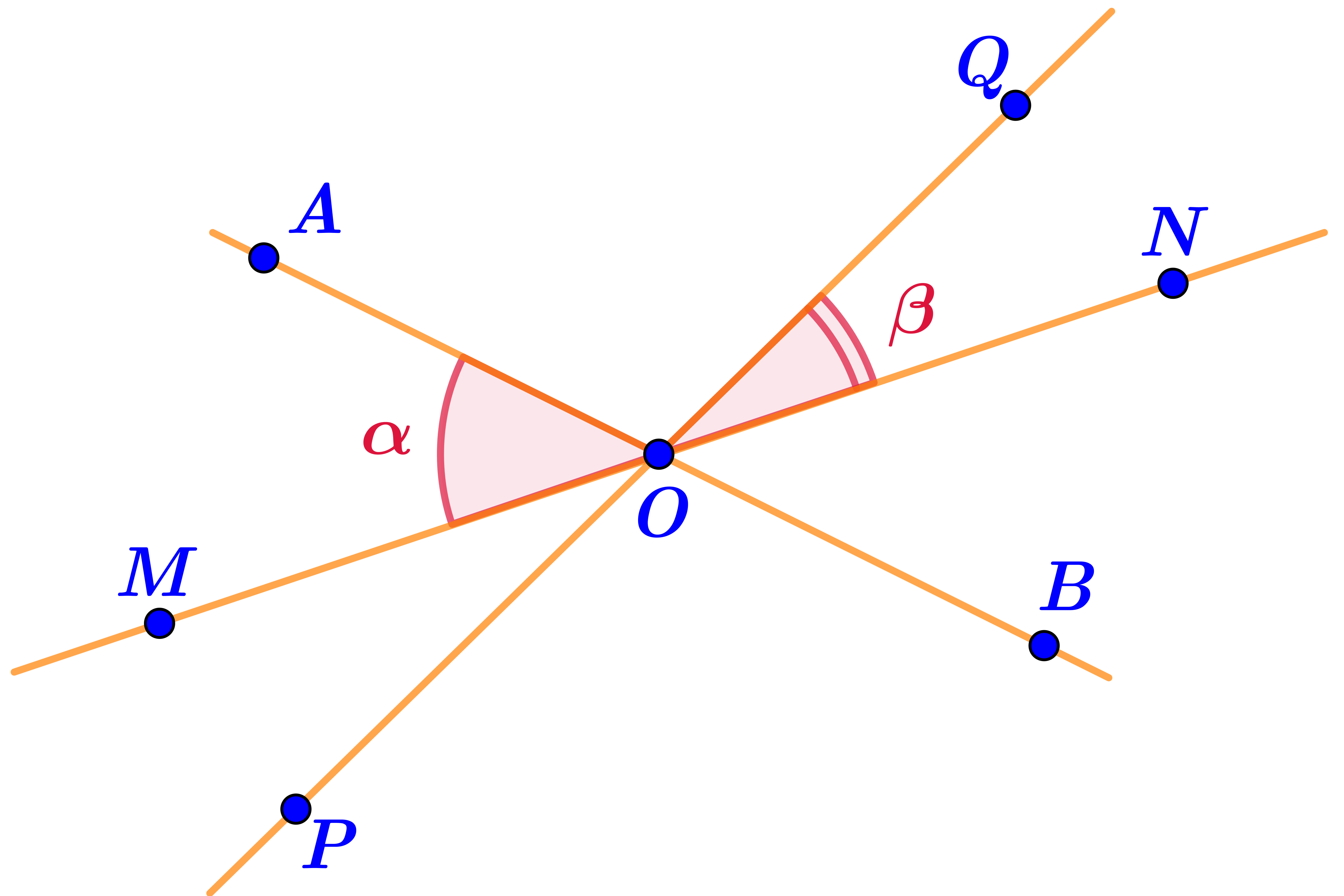
Известны величины отмеченных углов:
\(\displaystyle \alpha=33\degree {\small ,\;}\beta=19\degree {\small .}\)
Найти величину угла \(\displaystyle AOP{\small .}\)
\(\displaystyle \angle AOP=\)\(\displaystyle \degree \)
Искомый угол \(\displaystyle AOP\) разделён лучом \(\displaystyle OM\) на две части.
Значит, величина угла \(\displaystyle AOP\) равна сумме величин этих частей:
\(\displaystyle \angle AOP=\angle AOM+\angle MOP{\small .}\)
Угол \(\displaystyle AOM \) известен и равен \(\displaystyle \alpha{\small .} \) Найдём угол \(\displaystyle MOP{\small .}\)
Прямые \(\displaystyle MN\)и\(\displaystyle PQ \) содержат стороны угла \(\displaystyle MOP{\small .} \)
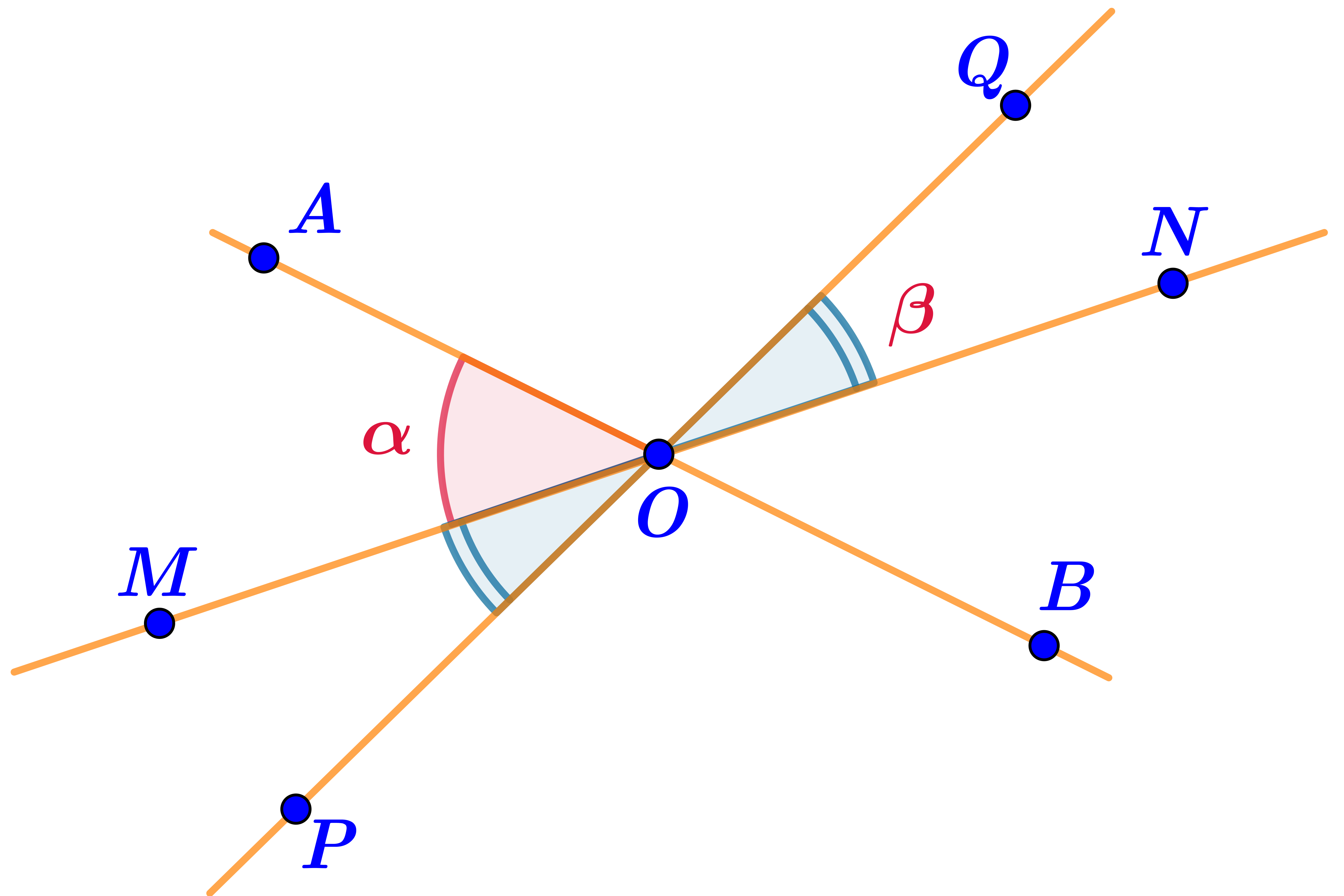
Значит, углы \(\displaystyle MOP\) и \(\displaystyle NOQ\) вертикальные и равны между собой:
\(\displaystyle \angle MOP=\angle NOQ=\beta{\small .}\)
Теперь величины обеих частей угла \(\displaystyle AOP\) известны:
\(\displaystyle \angle AOP=\angle MOP+\angle AOM=\alpha+\beta= 33\degree + 19\degree =52\degree {\small .}\)
Ответ: \(\displaystyle \angle AOP=52\degree {\small .}\)