Один из углов, образовавшихся при пересечении прямых \(\displaystyle a\) и \(\displaystyle b{ \small ,}\) поделили на \(\displaystyle 5\) равных частей величинами по \(\displaystyle 21\degree 24'\) каждая.
Другой \(\displaystyle -\) на \(\displaystyle 9\) равных частей (см. рисунок).
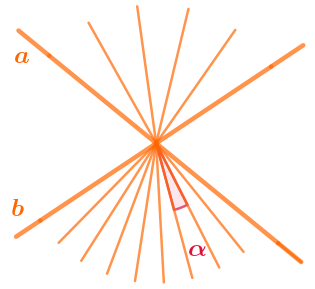
Выразите в градусах, минутах и секундах величину каждой из \(\displaystyle 9\) равных частей.
\(\displaystyle \alpha=\)\(\displaystyle \degree \)\(\displaystyle '\)\(\displaystyle ''\)
Чтобы найти величину искомого угла \(\displaystyle \alpha{\small ,}\) определим величину угла, образовавшегося при пересечении прямых \(\displaystyle a\) и \(\displaystyle b{\small ,}\) и поделенного на \(\displaystyle 9\) равных частей.
Величина этого угла равна:
\(\displaystyle 21\degree 24'\cdot 5=105\degree+120'=107\degree {\small ,}\)
поскольку \(\displaystyle 60\) минут составляют один градус.
Это угол образует пару вертикальных углов с тем, что делили на 5 частей.
Значит, его величина также равна \(\displaystyle 107\degree {\small .}\)
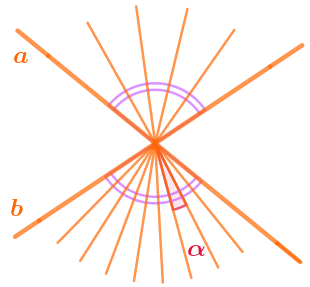
Эту величину нужно разделить на \(\displaystyle 9{\small .}\)
Чтобы это сделать, удобно представить величину угла в виде суммы кратного девяти числа градусов и переведённого в секунды остатка:
\(\displaystyle 107\degree = 99\degree +8\degree =99\degree + (8\cdot 60\cdot 60)''= 99\degree +28800''{\small .}\)
Теперь слагаемые \(\displaystyle -\) целые числа, кратные девяти. Значит:
\(\displaystyle \alpha=\frac{99\degree+28800''}{9}=11\degree +3200''=11\degree +3180''+20''=11\degree 53'20''\)
Ответ: \(\displaystyle 11\degree53' 20''{\small .}\)