Три прямые \(\displaystyle AF{\small ,\;}BD\) и \(\displaystyle CE\) пересекаются в точке \(\displaystyle O{\small .}\)
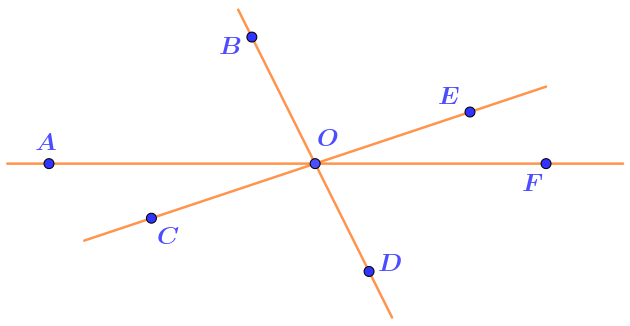
Какой угол вместе с углом \(\displaystyle EOD\) составляет пару вертикальных углов?
Два угла с общей вершиной называются вертикальными, если стороны каждого из них являются продолжениями (до прямой) сторон другого.
Любые два вертикальных угла равны между собой.
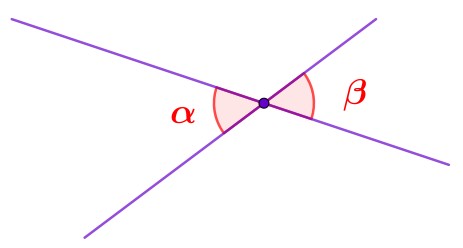
\(\displaystyle \alpha=\beta\)
Продлевая стороны угла \(\displaystyle EOD{\small ,}\) получим две пересекающиеся прямые \(\displaystyle CE\) и \(\displaystyle BD{\small .} \)
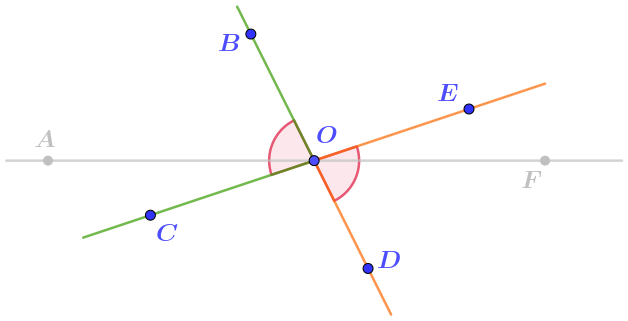
На рисунке найдём лучи, дополняющие до прямых обе стороны угла \(\displaystyle BOC{\text :}\)
- луч \(\displaystyle OD\) дополняется до прямой \(\displaystyle BD\) лучом \(\displaystyle OB{\text ;}\)
- луч \(\displaystyle OE\) дополняется до прямой \(\displaystyle CE\) лучом \(\displaystyle OC{\small .}\)
Значит, пару вертикальных углов с углом \(\displaystyle EOD\) составляет угол \(\displaystyle COB{\small .}\)
Ответ: \(\displaystyle \angle COB{\small .}\)