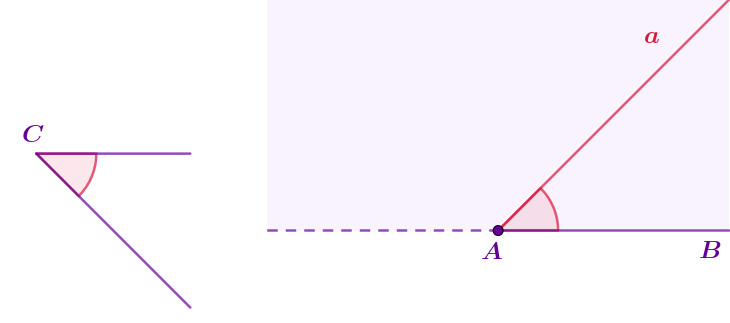
Лучи \(\displaystyle OA\) и \(\displaystyle OB\) дополняют друг друга до прямой.
От луча \(\displaystyle OA\) в одну из полуплоскостей относительно прямой \(\displaystyle AB\) отложен угол \(\displaystyle AOL\small .\)
От второго луча в другую полуплоскость отложен угол \(\displaystyle BON\) равный углу \(\displaystyle AOL\).
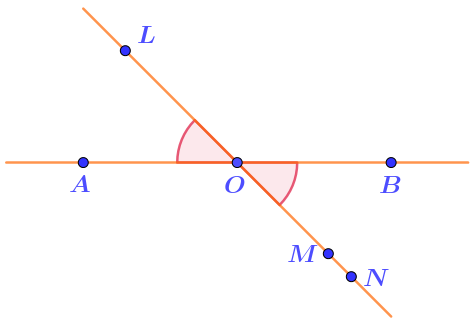
Составьте из фрагментов рассуждение, доказывающее, что точки \(\displaystyle L{\small ,\;}O\) и \(\displaystyle N\) принадлежат одной прямой.
| \(\displaystyle 1{\small .}\) | \(\displaystyle ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\) |
| \(\displaystyle 2{\small .}\) | \(\displaystyle ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\) |
| \(\displaystyle 3{\small .}\) | \(\displaystyle ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\) |
| \(\displaystyle 4{\small .}\) | \(\displaystyle ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\) |
\(\displaystyle ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\)
Он проходит по ту же сторону прямой \(\displaystyle AB{\small ,}\) что и луч \(\displaystyle ON{\small .}\)
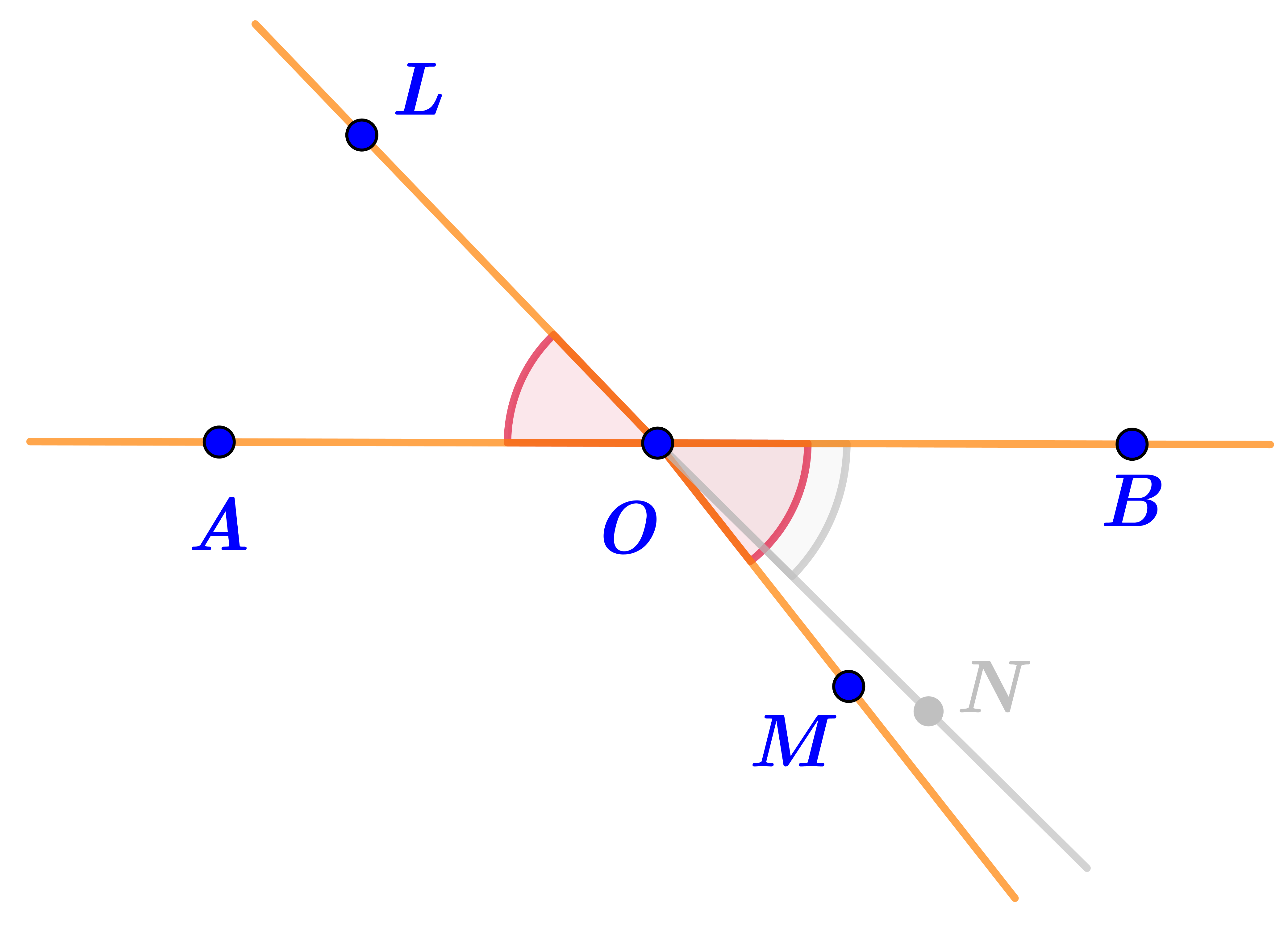
При этом образуется угол \(\displaystyle BOM{\small ,}\) вертикальный по определению к углу \(\displaystyle AOL{\small .}\)
Значит,
\(\displaystyle \angle AOL=\angle BOM{\small .}\)
2. Рассмотрим углы \(\displaystyle BON\) и \(\displaystyle BOM{\small .}\)
В данной задаче
\(\displaystyle \angle AOL=\angle BOM\) (по ранее доказаному)
и
\(\displaystyle \angle AOL=\angle BON\) (по условию задачи).
Значит,
\(\displaystyle \angle BON=\angle BOM{\small .}\)
Значит, \(\displaystyle OM\) и \(\displaystyle ON\) – один и тот же луч.
Тогда рисунок изменится на следующий:
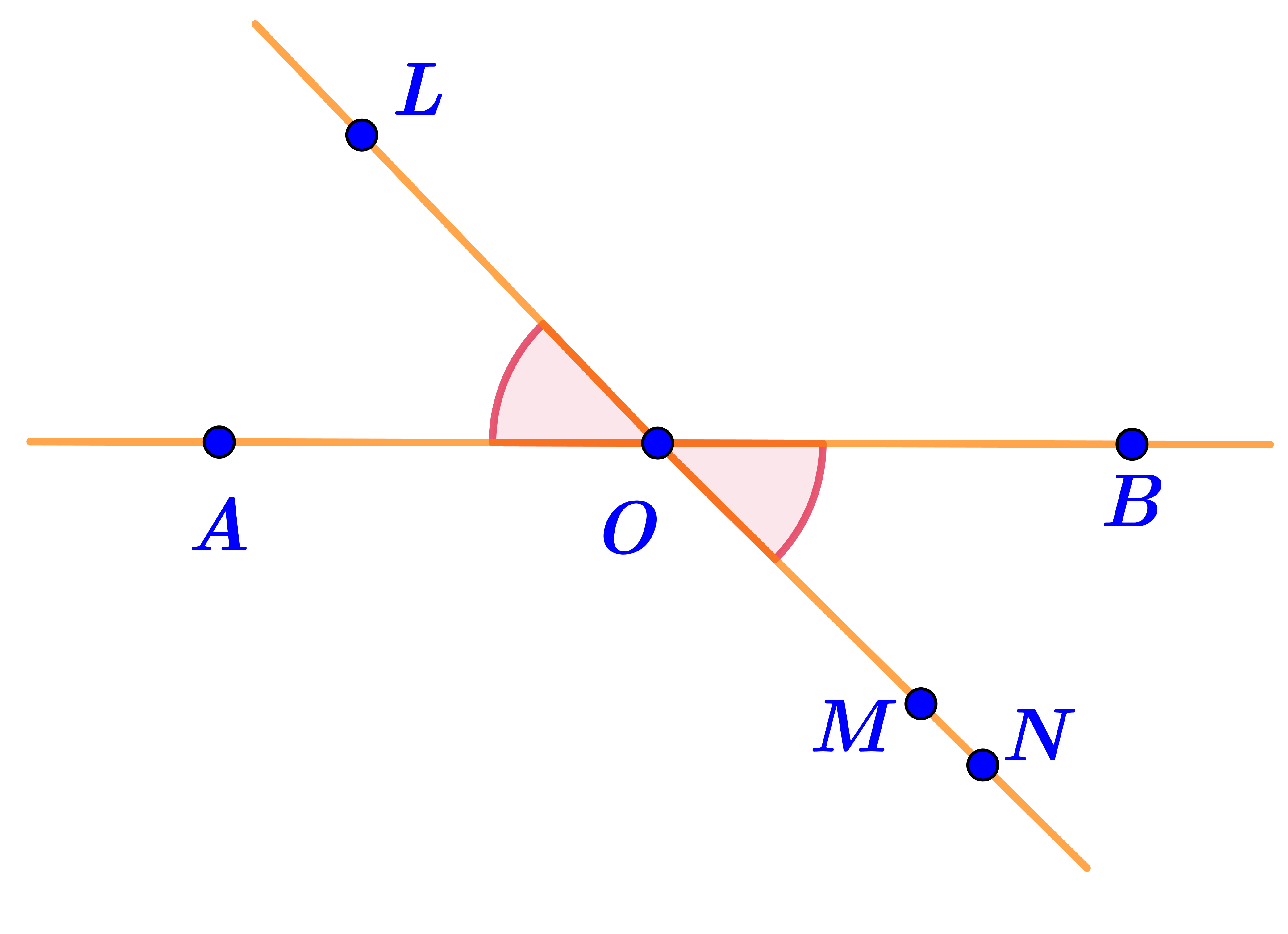
Все точки лучей \(\displaystyle OL\) и \(\displaystyle OM\) принадлежат одной прямой.
Значит, точки \(\displaystyle L{\small ,\;}O\) и \(\displaystyle N\) принадлежат одной прямой.
| Ответ: |  |