Skip to main content

Теория: Смежные углы

Задание

Три прямые \(\displaystyle AB,MN\) и \(\displaystyle PQ\) пересекаются в точке \(\displaystyle O{\small .}\)

 

 

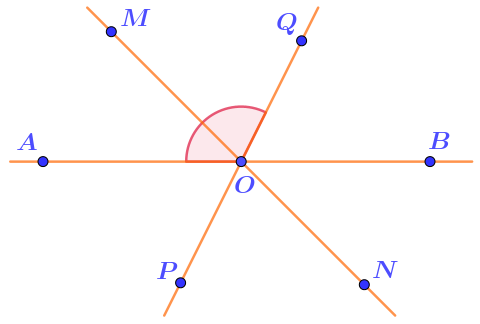
Выберите углы, смежные с углом \(\displaystyle AOQ{\small .}\)

Решение

1. Из определения следует, что для двух смежных углов всегда есть прямая, содержащая стороны обоих углов.

определение и свойство смежных углов

Два угла с общей вершиной называются смежными, если одна сторона у них общая, а две другие дополняют друг друга до прямой.

Сумма величин смежных углов равна ста восьмидесяти градусам.

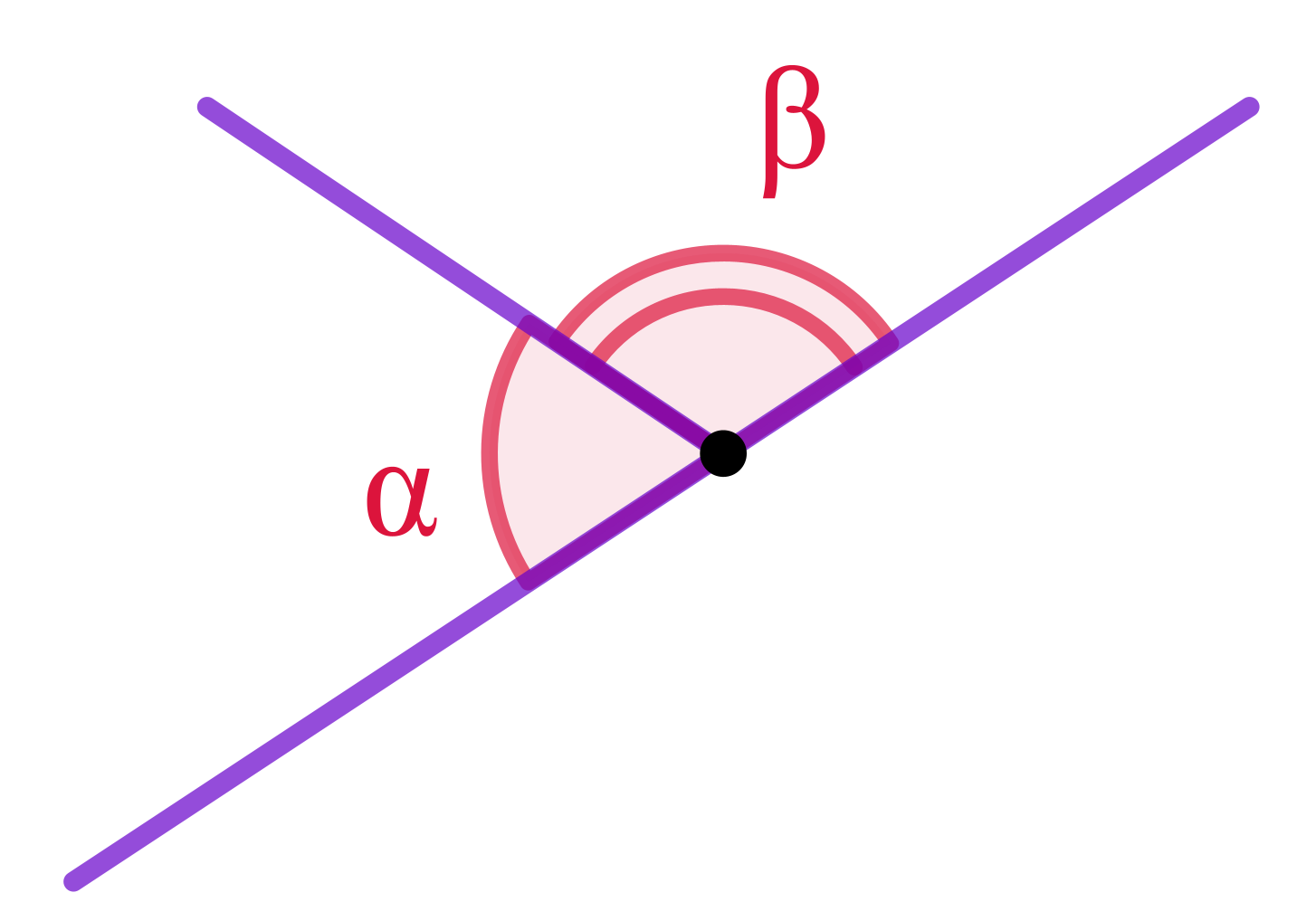
\(\displaystyle \alpha +\beta=180\degree\)

В нашем случае, стороны угла \(\displaystyle AOQ~-\) части прямых \(\displaystyle AB\) и \(\displaystyle QP{\small .}\)

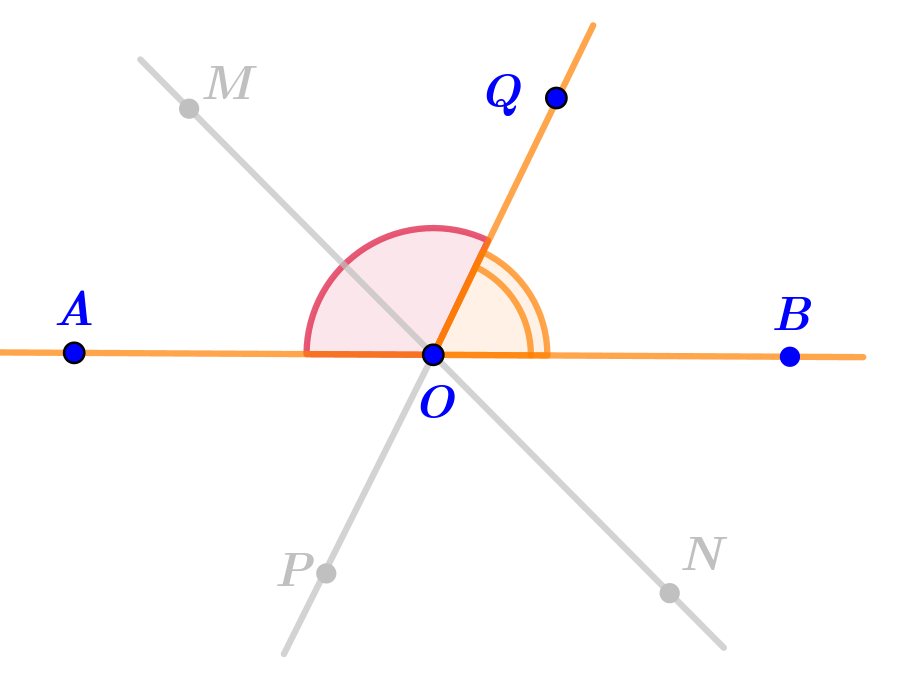
2. Начнём с прямой \(\displaystyle AB{ \small ,} \) которая содержит сторону \(\displaystyle OA\) угла \(\displaystyle AOQ{\small .} \)

 

До этой прямой сторону \(\displaystyle OA\) угла \(\displaystyle AOQ\) дополняет луч \(\displaystyle OB{\small .}\) 

Тогда угол \(\displaystyle QOB{\small ,}\) составленный из лучей \(\displaystyle OQ\) и \(\displaystyle OB{\small ,}\) является смежным с углом \(\displaystyle AOQ\) по определению.

3. Второй смежный с углом \(\displaystyle AOQ\) угол также есть на рисунке.  Это угол \(\displaystyle AOP{\small .}\)

На этот раз рассмотрим прямую \(\displaystyle QP{ \small ,} \) содержащую сторону \(\displaystyle OQ \) угла \(\displaystyle AOQ{\small .} \)

 

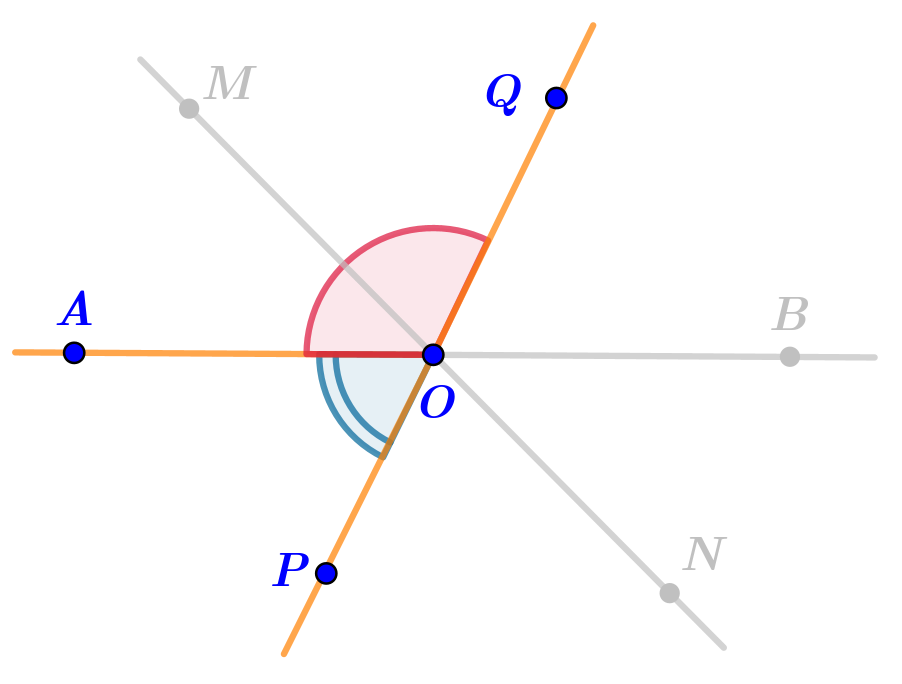
До этой прямой сторону \(\displaystyle OQ\) угла \(\displaystyle AOQ\) дополняет луч \(\displaystyle OP{\small .}\) 

Тогда угол \(\displaystyle AOP\) является смежным с углом \(\displaystyle AOQ\) по определению.

Замечание / комментарий

У любого угла две стороны, которые, при условии, что угол не является развёрнутым, дополняются до двух прямых.

Значит для любого неразвёрнутого угла можно построить ровно два смежных с ним угла.

Ответ: \(\displaystyle AOP,\,QOB{\small .}\)