Величина одного из двух смежных углов на \(\displaystyle 32\degree \) больше величины другого.
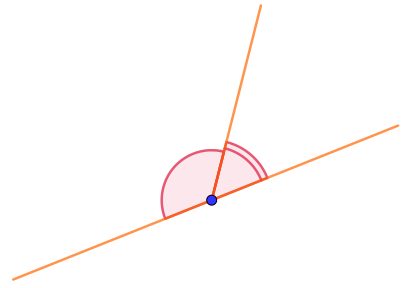
Выразите в градусах величину большего из них.
\(\displaystyle \degree {\small .}\)
Два угла с общей вершиной называются смежными, если одна сторона у них общая, а две другие дополняют друг друга до прямой.
Сумма величин смежных углов равна ста восьмидесяти градусам.
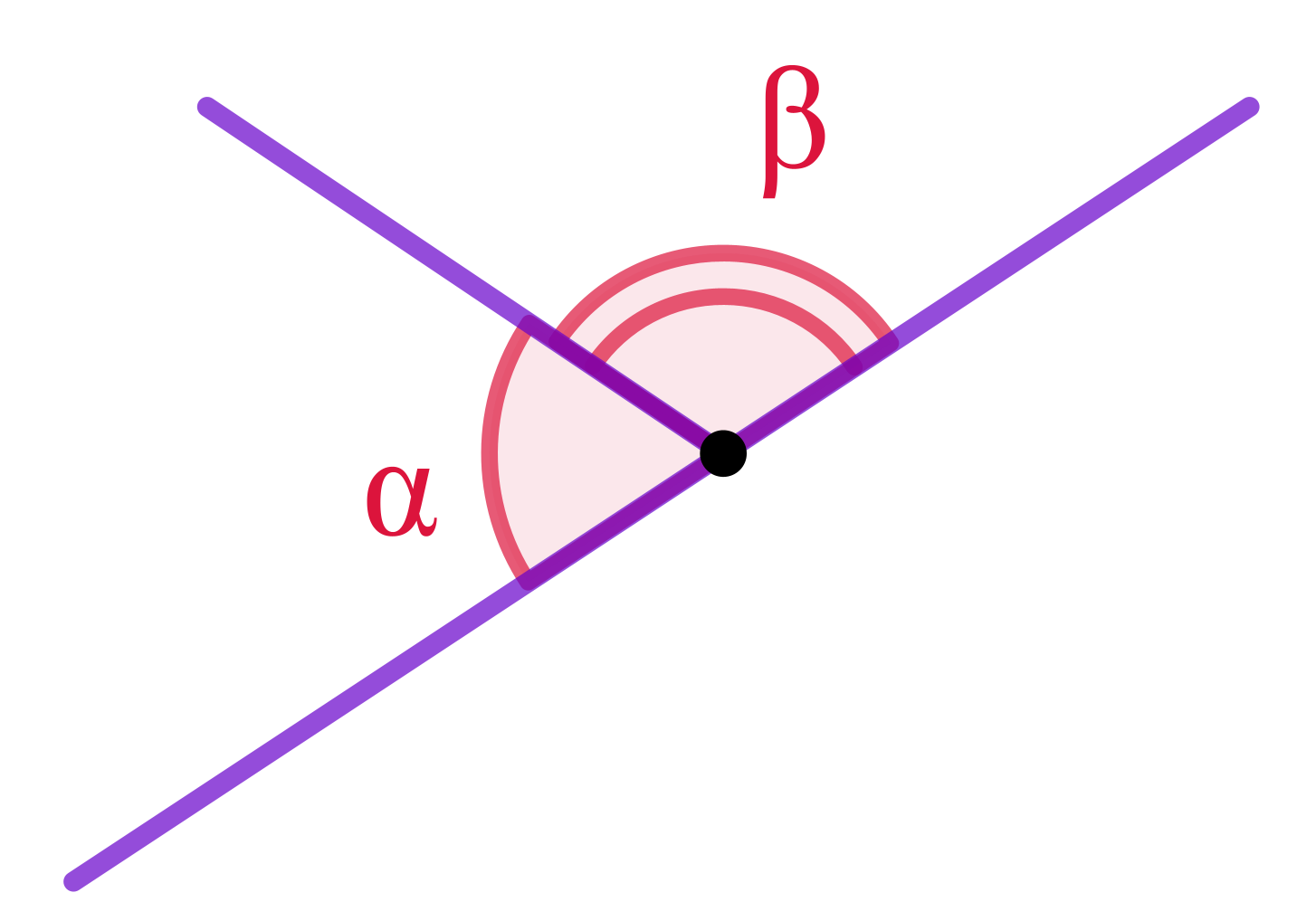
\(\displaystyle \alpha +\beta=180\degree\)
Обозначим через \(\displaystyle \beta\) искомую величину большего из двух смежных углов.
Тогда величину меньшего угла можно записать как \(\displaystyle 180\degree-\beta{\small .}\)
Запишем это в виде уравнения:
\(\displaystyle \beta-32\degree =180\degree -\beta{\small .}\)
Перенесём неизвестные в одну часть, а числа в другую:
\(\displaystyle 2\beta=212\degree {\small .}\)
Делим на два и получаем ответ:
\(\displaystyle \beta=106\degree{\small .}\)
Ответ: \(\displaystyle 106\degree{\small .}\)