Дополните таблицу величин смежных углов.
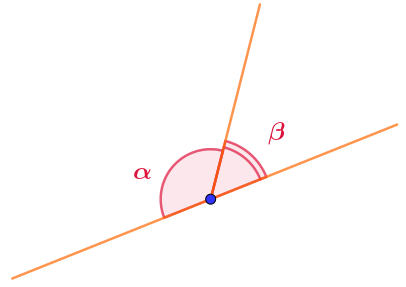
Величина угла \(\displaystyle \alpha\) | Величина угла \(\displaystyle \beta\) |
\(\displaystyle 40\degree \) | \(\displaystyle \degree \) |
\(\displaystyle 90\degree \) | \(\displaystyle \degree \) |
\(\displaystyle 133\degree \) | \(\displaystyle \degree \) |
\(\displaystyle 28\degree 35'\) | \(\displaystyle \degree \)\(\displaystyle '\) |
\(\displaystyle 99\degree 17'~52''\) | \(\displaystyle \degree \)\(\displaystyle '\)\(\displaystyle ''\) |
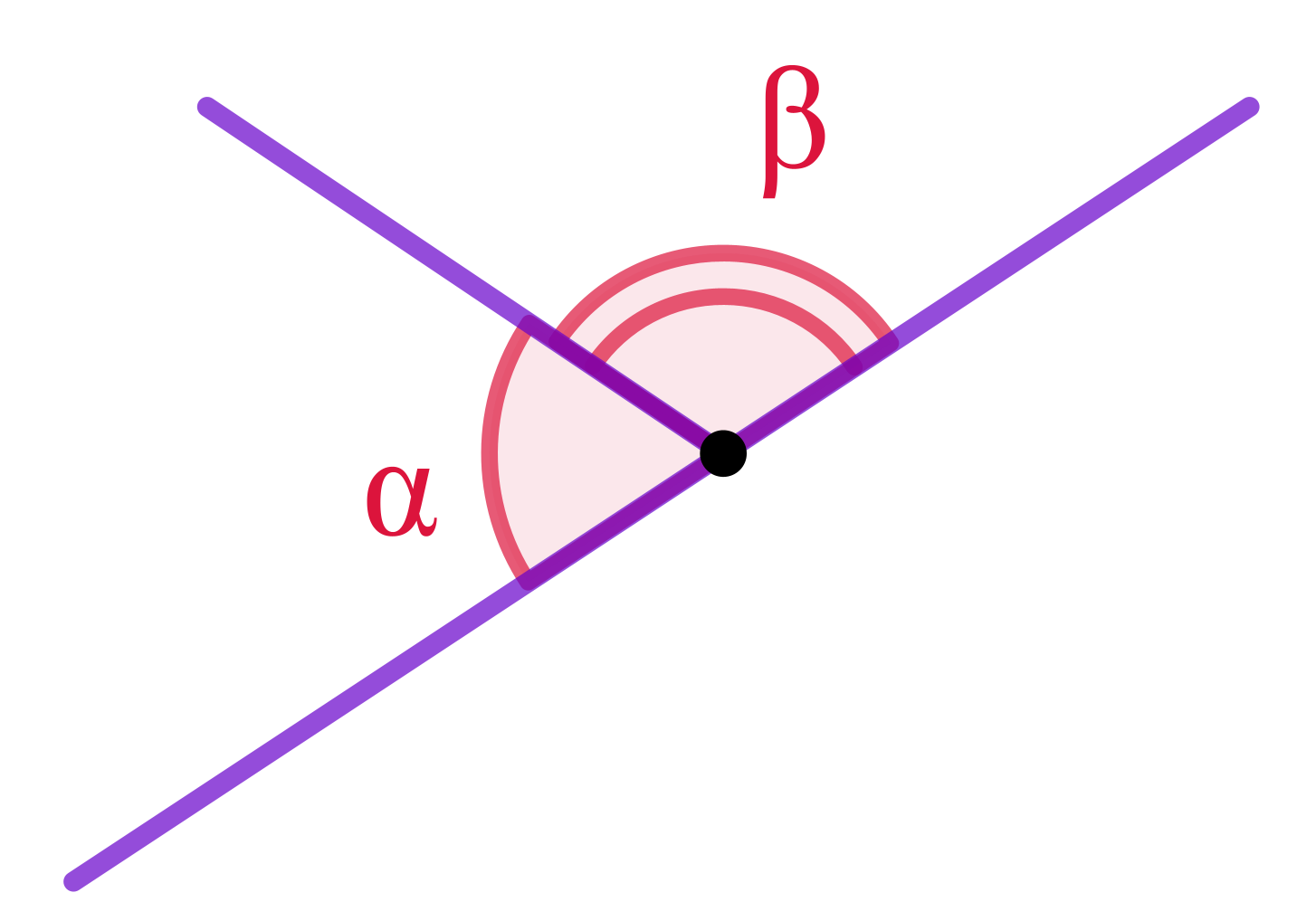
На рисунке \(\displaystyle \alpha\) и \(\displaystyle \beta\) – смежные углы.
По свойству смежных углов, сумма их величин равна \(\displaystyle 180\degree{\small .}\)
\(\displaystyle \beta=180\degree - 40\degree= 140\degree{\small .}\)
В одном градусе содержится \(\displaystyle 60\) минут:
\(\displaystyle 1\degree=60'{\small .}\)
Поэтому:
\(\displaystyle \beta=180\degree -28\degree 35'=179 \degree+60' -28\degree- 35' =151\degree25'{\small .}\)
| Ответ: | 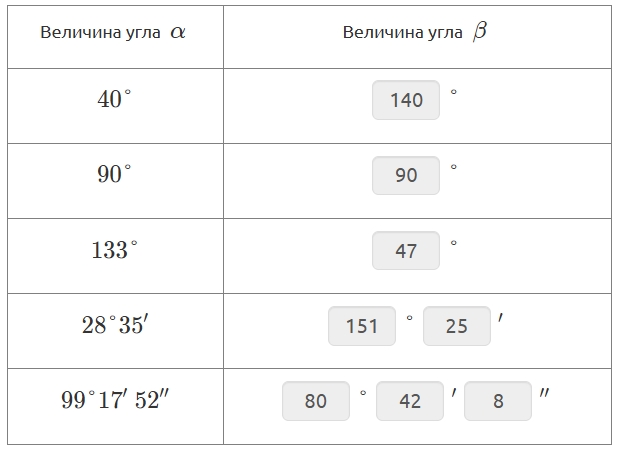 |