Задание
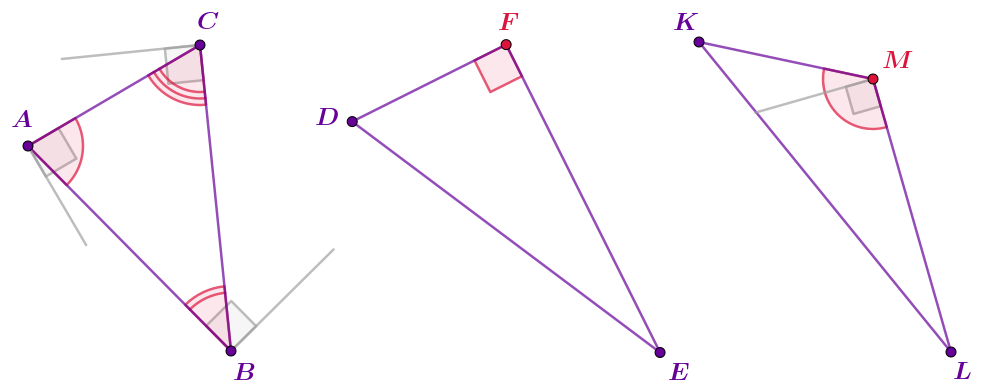
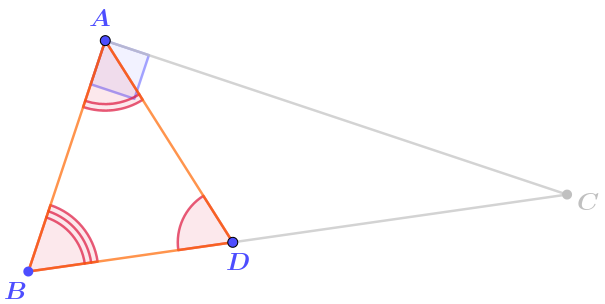
На плоскости отмечены точки \(\displaystyle A,\,B,\,C,\,D\) и соединены отрезками. При этом образовались прямой угол \(\displaystyle BAC\) и острый угол \(\displaystyle ADB{\small .}\)
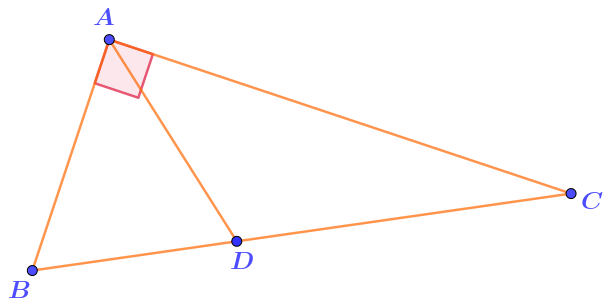
Сопоставьте трём образовавшимся треугольникам их вид.
| \(\displaystyle {\bf\triangle} ABC\) | \(\displaystyle -\) | |
| \(\displaystyle {\bf\triangle}ACD\) | \(\displaystyle -\) | |
| \(\displaystyle {\bf\triangle}ABD\) | \(\displaystyle -\) |
Решение
Последовательно опредляем вид треугольников, пользуясь определениями остроугольного, тупоугольного и прямоугольного треугольников.
Треугольник \(\displaystyle ABC\) прямоугольный.
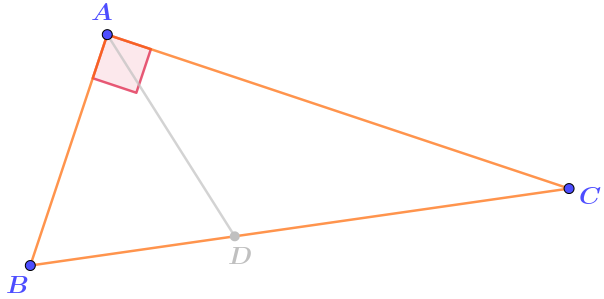
Для того чтобы это показать, достаточно найти в нём прямой угол.
Угол \(\displaystyle BAC\) при вершине \(\displaystyle A\) прямой по условию.
Треугольник \(\displaystyle ACD\) тупоугольный.
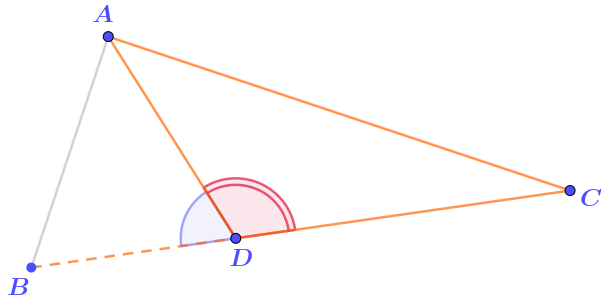
Для того чтобы это показать, достаточно найти в нём тупой угол.
Угол \(\displaystyle ADC\) является смежным к острому по условию углу \(\displaystyle ADB{\small .}\)
То есть тупым.
Треугольник \(\displaystyle ABD\) остроугольный
Для того чтобы это показать, нужно убедиться, что все три его угла острые.
- Угол \(\displaystyle ADB\) острый по условию.
- Угол \(\displaystyle BAD\) острый, так как является частью прямого по условию угла \(\displaystyle BAC{\small .}\)
- Угол \(\displaystyle ABD\) острый, так как является углом прямоугольного треугольника \(\displaystyle ABC{\small ,}\) но не прямым его углом.
| Ответ: | 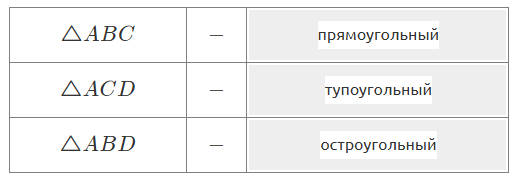 |