На стороне \(\displaystyle AB\) прямоугольного треугольника \(\displaystyle ABC\) отмечены точки \(\displaystyle H\) и \(\displaystyle K{\small .}\)
Проведены отрезки \(\displaystyle CH\) и \(\displaystyle CK{\small .}\)
Угол \(\displaystyle CHK\) прямой.
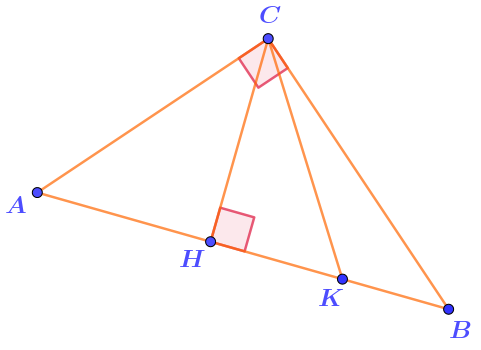
Сколько углов каждого вида в образовавшихся треугольниках?
Тупых углов | Прямых углов | Острых углов | |
В треугольнике \(\displaystyle ACK\) | |||
В треугольнике \(\displaystyle BCK\) | |||
В треугольнике \(\displaystyle ACH\) |
Из двух прилежащих к одной стороне углов треугольника один обязательно острый.
Из этого следует, что два из трёх углов треугольника обязательно острые.
Поэтому:
- в остроугольном треугольнике три острых угла;
- в прямоугольном треугольнике один прямой и два острых угла;
- в тупоугольном треугольнике один тупой и два острых угла.
Рассмотрим три угла этого треугольника.
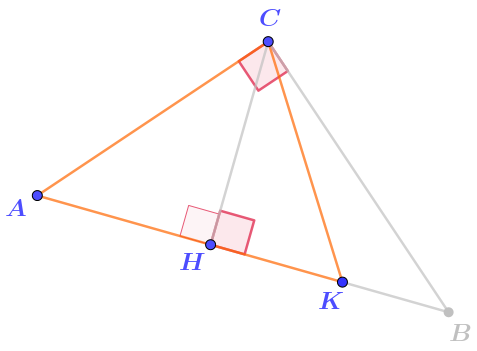
- Угол \(\displaystyle ACK\) часть прямого угла \(\displaystyle ACB{ \small ,}\) то есть острый по определению.
- Угол \(\displaystyle AKC\) является углом прямоугольного треугольника \(\displaystyle KCH\) с прямым углом \(\displaystyle CHK{\small .}\) Значит, он острый по свойству прямоугольного треугольника.
- Угол \(\displaystyle CAK\) острый по той же причине: он является углом прямоугольного треугольника \(\displaystyle ACH\) с прямым углом \(\displaystyle AHC{\small .}\) Этот угол прямой, так как смежен с прямым углом \(\displaystyle CHK{\small .}\)
Угол \(\displaystyle BKC\) тупой, так как является смежным острому углу \(\displaystyle AKC\) остроугольного треугольника \(\displaystyle ACK{\small .}\)
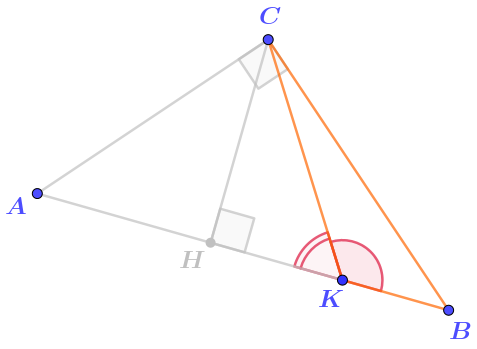
Значит, треугольник \(\displaystyle BKC\) тупоугольный.
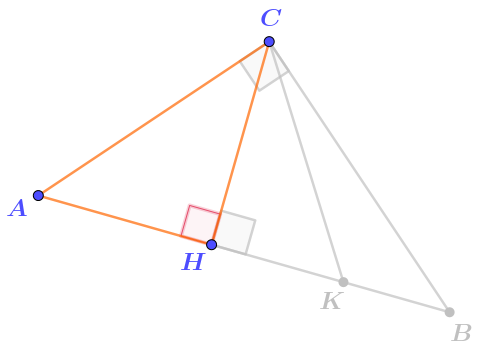
Ответ:
