На стороне \(\displaystyle AC\) треугольника \(\displaystyle ABC\) отмечена точка \(\displaystyle M\) так, что \(\displaystyle AM:MC=2:3\small.\) Из точки \(\displaystyle M\) проведена прямая, параллельная стороне \(\displaystyle AB\) и пересекающая сторону \(\displaystyle BC\) в точке \(\displaystyle N\small.\) Аналогично, получена точка \(\displaystyle K\) на стороне \(\displaystyle AB\small.\) Во сколько раз площадь треугольника \(\displaystyle ABC\) больше площади четырехугольника \(\displaystyle MKBN\small?\)
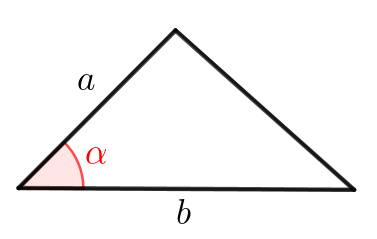
Площадь треугольника \(\displaystyle ABC\) можно найти по формуле: \(\displaystyle S_{ABC}=\frac{1}{2}AB\cdot BC \cdot \sin\angle ABC\small.\)
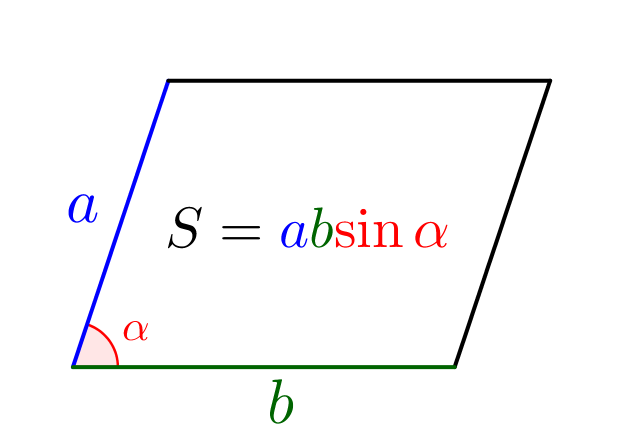
Площадь параллелограмма \(\displaystyle KBNM\) можно найти по формуле: \(\displaystyle S_{KBNM}=KB\cdot BN \cdot \sin\angle KBN\small.\) | 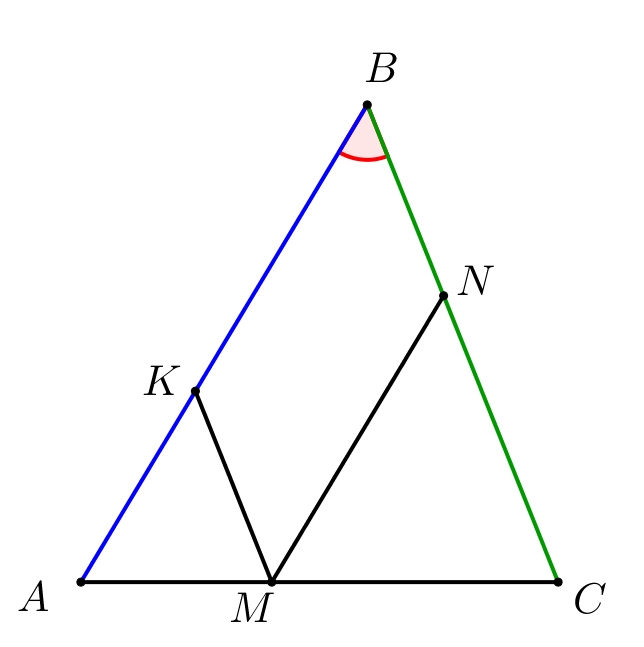 |
Тогда, чтобы найти отношение площадей треугольника и параллелограмма, найдем \(\displaystyle \frac{BC}{BN}\) и \(\displaystyle \frac{AB}{KB}\small.\)
Прямые \(\displaystyle AB\) и \(\displaystyle MN\) параллельны.
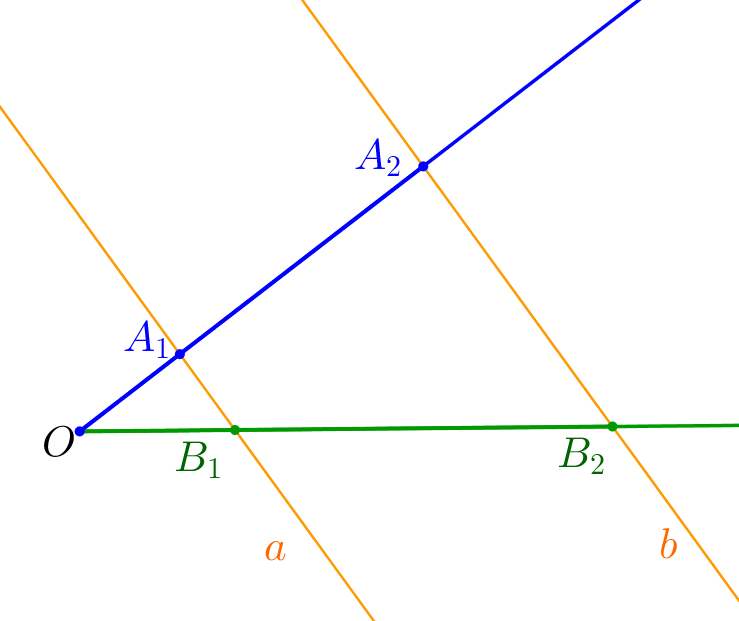
По теореме о пропорциональных отрезках \(\displaystyle \frac{BN}{NC}=\frac{AM}{MC}=\frac{2}{3}\small.\) Значит, \(\displaystyle \frac{BC}{BN}=\frac{BN+NC}{BN}=1+\frac{3}{2}=\frac{5}{2}\small.\) | 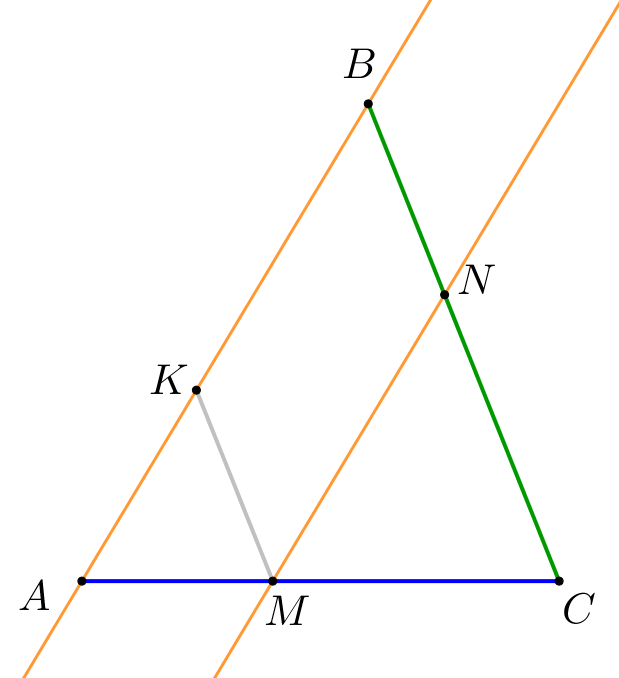 |
Прямые \(\displaystyle BC\) и \(\displaystyle KM\) параллельны.
По теореме о пропорциональных отрезках \(\displaystyle \frac{AK}{KB}=\frac{AM}{MC}=\frac{2}{3}\small.\) Значит, \(\displaystyle \frac{AB}{KB}=\frac{AK+KB}{KB}=\frac{2}{3}+1=\frac{5}{3}\small.\) | 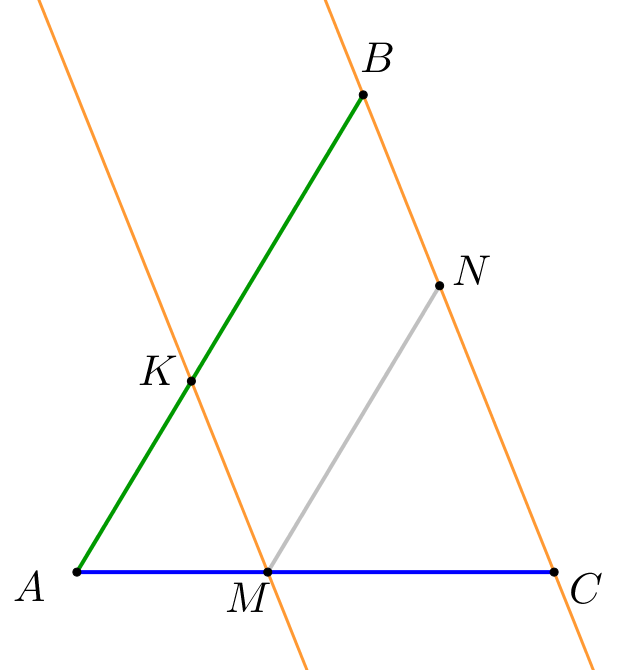 |
Учитывая полученные соотношения, вычислим, во сколько раз площадь треугольника \(\displaystyle ABC\) больше площади четырехугольника \(\displaystyle MKBN\small{:}\)
\(\displaystyle \frac{S_{ABC}}{S_{KBNM}}=\frac{\frac{1}{2}AB\cdot BC \cdot \cancel{\sin\angle ABC}}{KB\cdot BN \cdot \cancel{\sin\angle KBN}}=\frac{1}{2}\cdot\frac{5}{3}\cdot\frac{5}{2}=\frac{25}{12}\small.\)
Ответ: \(\displaystyle \frac{25}{12}\small.\)