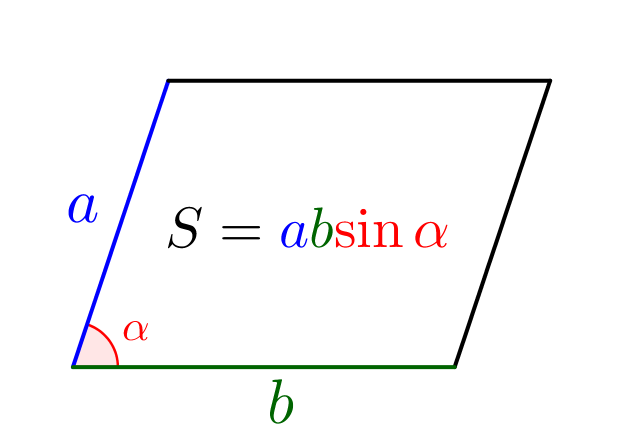
Трапеция \(\displaystyle ABCD\) изображена на рисунке. Известно, что \(\displaystyle AB=6,\,BC=7\) и \(\displaystyle \angle BAD=45^\circ\small.\) Найдите \(\displaystyle AD\small,\) если площадь трапеции \(\displaystyle 30\sqrt{2}\small.\)
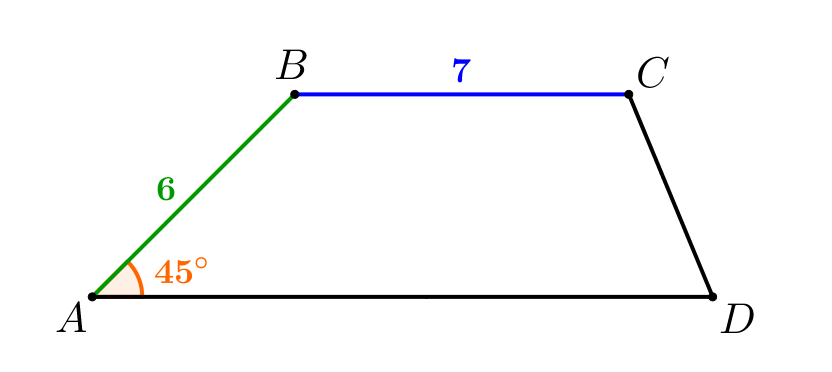
Проведем через \(\displaystyle C\) отрезок \(\displaystyle CN\small,\) параллельный \(\displaystyle AB\small.\) Тогда в четырехугольнике \(\displaystyle ABCN\) любые две противоположные стороны параллельны. То есть \(\displaystyle ABCN\) - параллелограмм.
Найдем его площадь: \(\displaystyle S_{ABCN}=AB\cdot AN\cdot\sin\angle 45^{\circ}=21\sqrt{2}\small.\) | 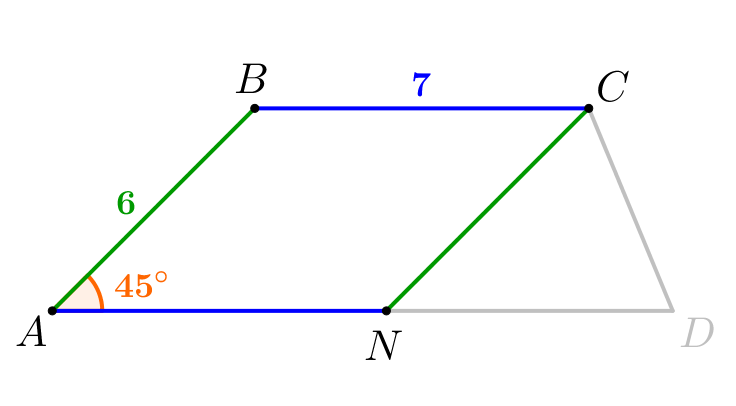 |
Найдем площадь треугольника \(\displaystyle CDN\small.\) Для этого вычтем из площади трапеции площадь параллелограмма:
\(\displaystyle S_{CDN}=S_{ABCD}-S_{ABCN}=30\sqrt{2}-21\sqrt{2}=9\sqrt{2}\small.\)
Теперь, зная площадь треугольника \(\displaystyle CDN\small,\) найдем его сторону \(\displaystyle ND\small.\) Так как \(\displaystyle AB\) параллелен \(\displaystyle CN\small,\) то соответственные углы равны: \(\displaystyle \angle BAN=\angle CND=45^{\circ}\small.\) Подставляя в формулу площади треугольника, получаем: \(\displaystyle S_{CDN}=\frac{1}{2}\cdot NC\cdot ND\cdot\sin45^{\circ}\small.\) | 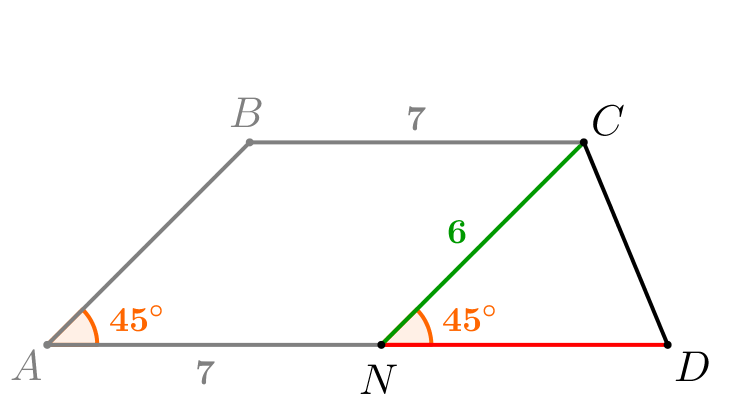 |
Подставим известные значения \(\displaystyle CN=AB=6,\,S_{CDN}=9\sqrt{2}\) и \(\displaystyle \sin45^{\circ}=\frac{\sqrt{2}}{2}{\small:}\)
\(\displaystyle 9\sqrt{2}=\frac{1}{2}\cdot6\cdot ND\cdot\frac{\sqrt{2}}{2}\small,\)
\(\displaystyle ND=9\sqrt{2}:\left(\frac{6\sqrt{2}}{4}\right)=6\small.\)
Тогда
\(\displaystyle AD=AN+ND=BC+ND=7+6=13 \small.\)
Ответ: \(\displaystyle AD=13 \small.\)
Рассмотрим план другого способа решения.
Проведем высоту \(\displaystyle BH\small.\) Зная гипотенузу \(\displaystyle AB\) и угол \(\displaystyle BAH\) в прямоугольном треугольнике \(\displaystyle ABH\small,\) можно найти \(\displaystyle BH\small.\) Площадь трапеции равна произведению полусуммы оснований и высоты. Значит, зная высоту трапеции, площадь и одно из оснований, можно найти второе. | 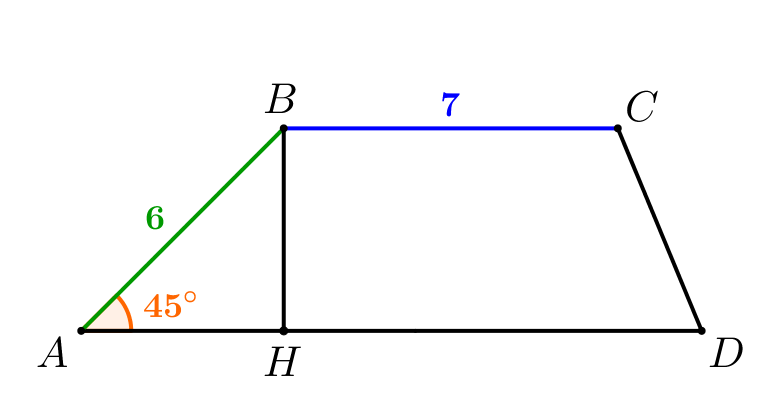 |