Диагонали четырехугольника \(\displaystyle ABCD\) равны \(\displaystyle 5\) и \(\displaystyle 8{ \small}\) и пересекаются под углом \(\displaystyle \alpha=30^{\circ}\small.\) Найдите площадь четырехугольника, образованного серединами сторон \(\displaystyle ABCD\small.\)
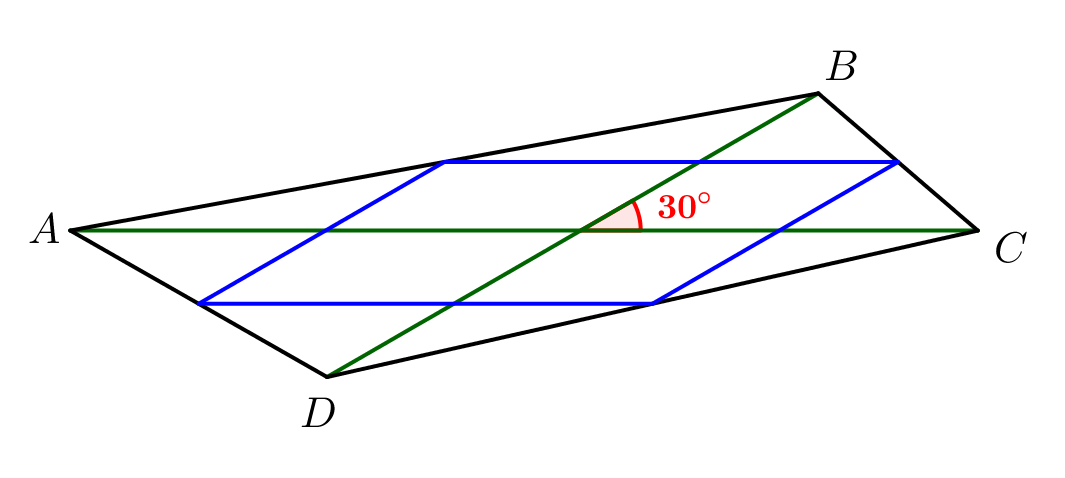
Обозначим середины сторон четырехугольника точками \(\displaystyle K,\,L,\,M,\,N\small.\)
Тогда \(\displaystyle KL\) – средняя линия треугольника \(\displaystyle ABC\small,\) а \(\displaystyle MN\) – средняя линия \(\displaystyle ACD\small.\) Значит, \(\displaystyle KL||AC||MN\) и \(\displaystyle KL=MN=\frac{1}{2}AC=4\small.\) | 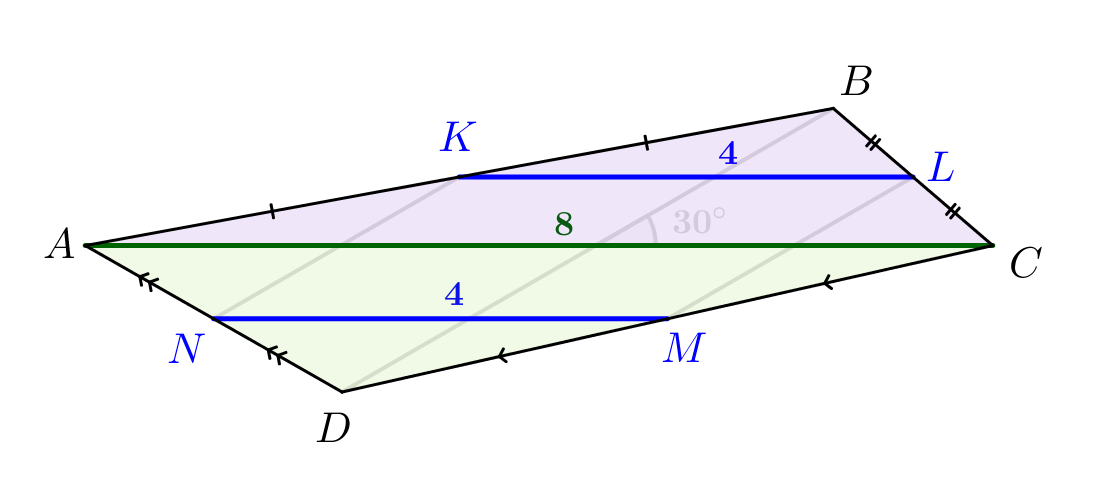 |
Аналогично, \(\displaystyle LM\) – средняя линия \(\displaystyle BCD\small,\) и \(\displaystyle KN\) – средняя линия \(\displaystyle BAD\small.\) Значит, \(\displaystyle LM||BD||KN\) и \(\displaystyle LM=KN=\frac{1}{2}BD=2{,}5\small.\) | 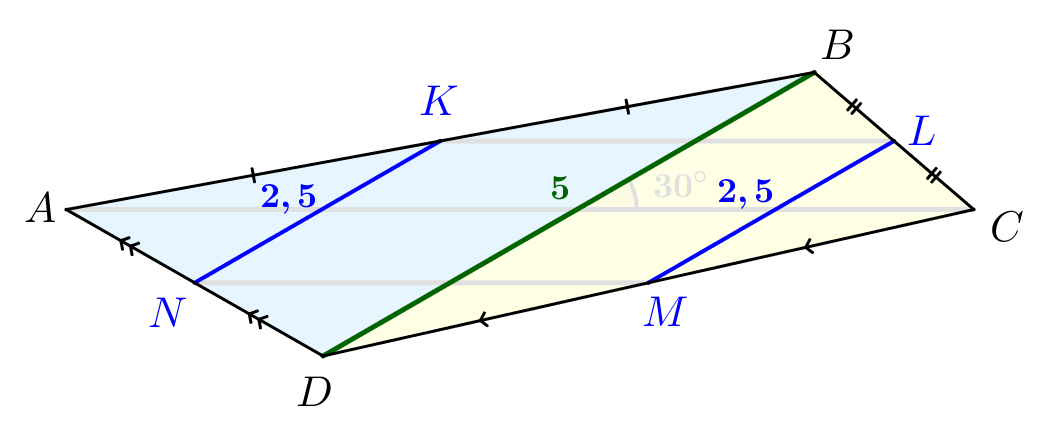 |
В четырехугольнике \(\displaystyle KLMN\) противоположные стороны равны и параллельны. Значит, \(\displaystyle KLMN\) – параллелограмм.
Также отметим равные углы.
Так как \(\displaystyle AC||MN\small,\) то углы \(\displaystyle BPM\) и \(\displaystyle BOC\) равны как соответственные: \(\displaystyle \angle BPM= \angle BOC =30^\circ\small.\) Аналогично, так как \(\displaystyle BD||KN\small,\) то углы \(\displaystyle KNM\) и \(\displaystyle BPM\) равны как соответственные: \(\displaystyle \angle KNM= \angle BPM =30^\circ\small.\) | 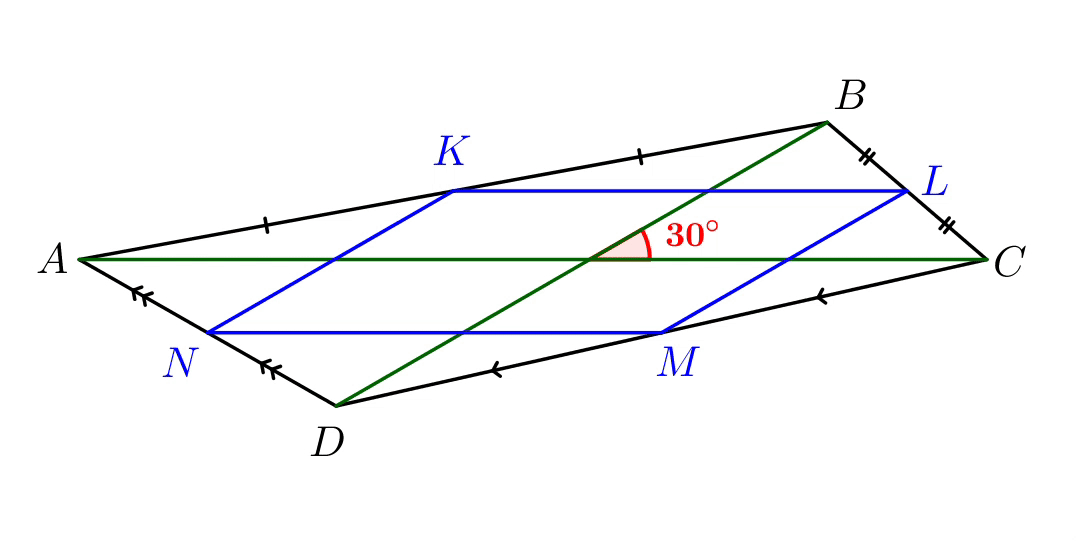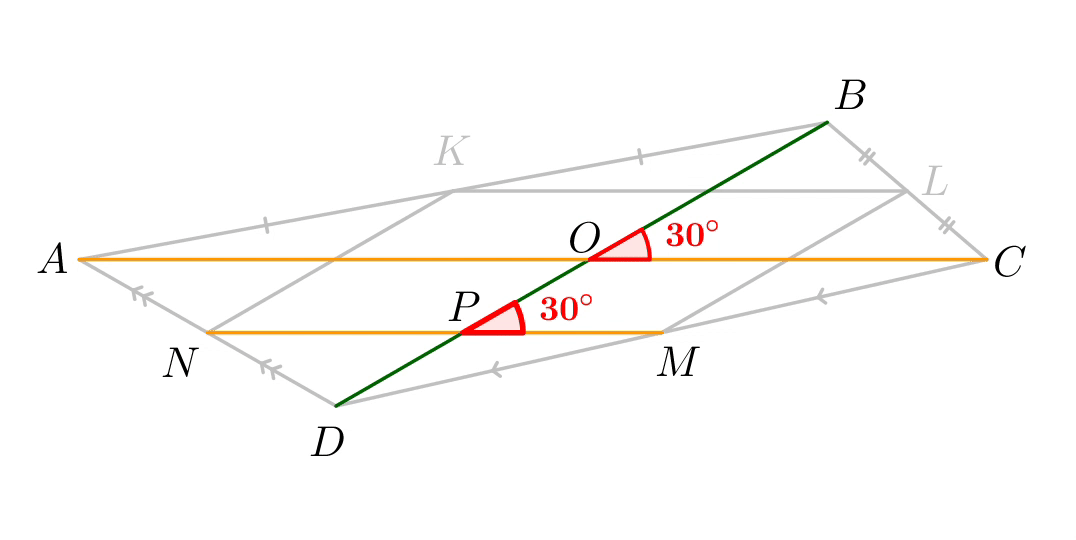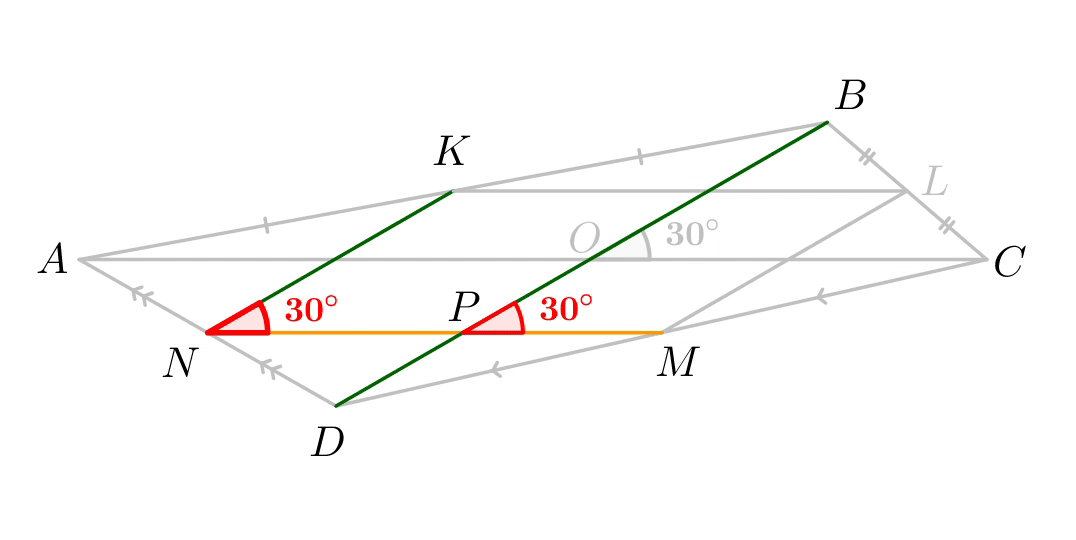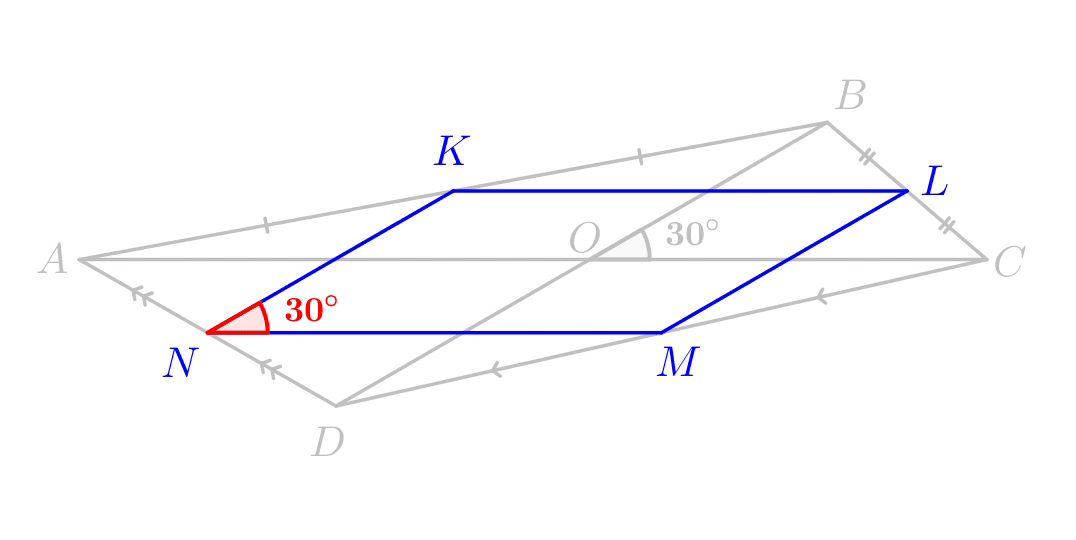 |
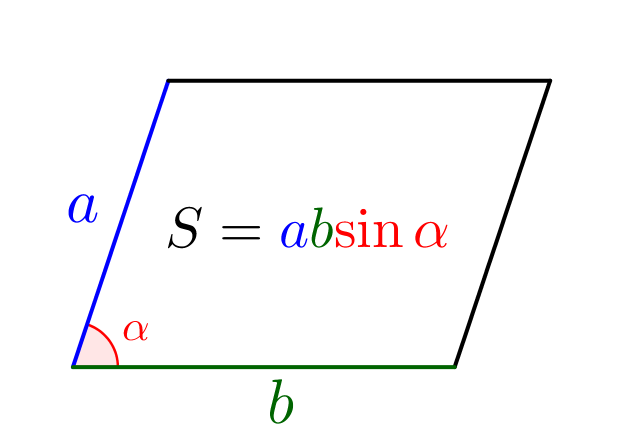
\(\displaystyle S_{KLMN}=KN\cdot NM\cdot \sin \angle KNM=2{,}5\cdot 4\cdot \frac{1}{2}=5\small.\)
Ответ: \(\displaystyle S_{KLMN}=5\small.\)