Стороны \(\displaystyle AB\) и \(\displaystyle BC\) прямоугольника \(\displaystyle ABCD\) равны сторонам \(\displaystyle MN\) и \(\displaystyle NK\) параллелограмма \(\displaystyle MNKP\small.\) При этом площадь прямоугольника в два раза больше площади параллелограмма. Чему равен острый угол параллелограмма \(\displaystyle MNKP\small?\)
Обозначим острый угол параллелограмма, который нужно найти, за \(\displaystyle \color{red}\alpha\small.\)
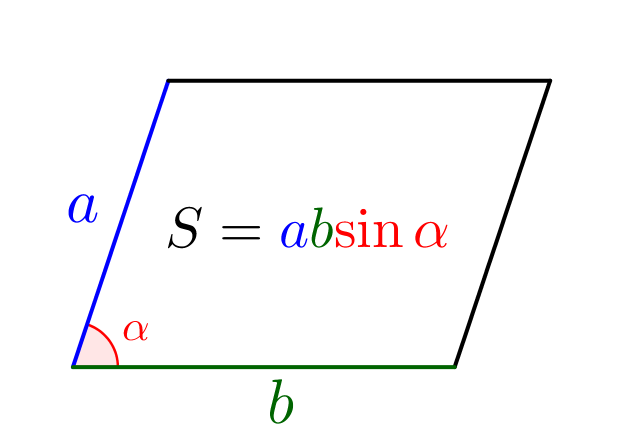
Площадь параллелограмма \(\displaystyle MNKP\) можно найти по формуле: \(\displaystyle S_{MNKP}=MN\cdot NK\cdot \sin \color{red}\alpha\small.\) | 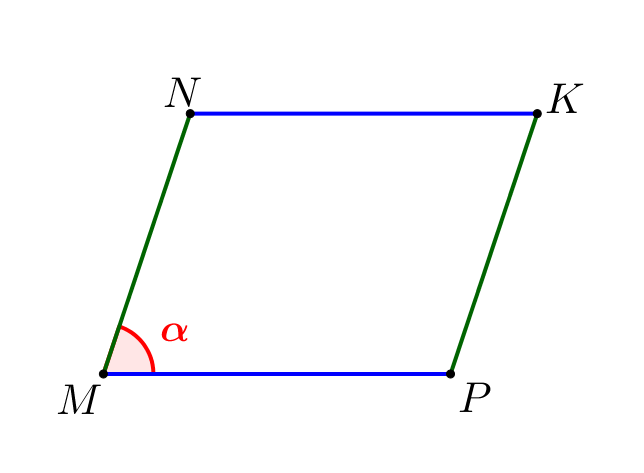 |
Площадь прямоугольника равна произведению длин его смежных сторон: \(\displaystyle S_{ABCD}=AB\cdot BC\small.\) | 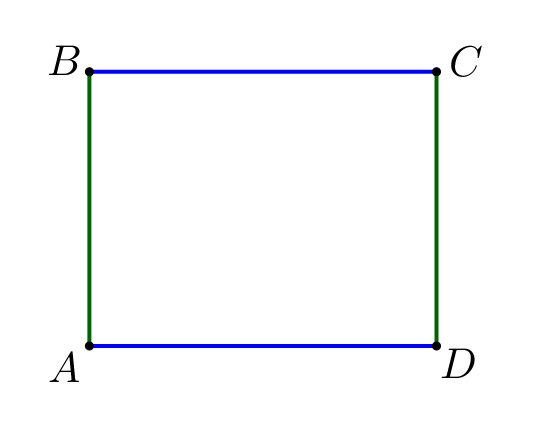 |
По условию, площади отличаются в два раза. При этом формулы вычисления площадей отличаются в \(\displaystyle \sin \color{red}\alpha\small.\)
Тогда, сравнивания площади, найдем \(\displaystyle \sin \color{red}\alpha\small.\)
Отношение площадей равно:
\(\displaystyle \frac{S_{ABCD}}{S_{MNKP}}=\frac{AB\cdot BC}{MN\cdot NK\cdot \sin \color{red}\alpha}=2\small.\)
Перепишем это равенство, учитывая, что \(\displaystyle AB=MN\) и \(\displaystyle BC=NK\small{:}\)
\(\displaystyle \frac{AB\cdot BC}{MN\cdot NK\cdot \sin \color{red}\alpha}=\frac{\cancel{MN}\cdot \cancel{NK}}{\cancel{MN}\cdot \cancel{NK}\cdot \sin \color{red}\alpha}=2\small,\)
\(\displaystyle \frac{1}{\sin \color{red}\alpha}=2\small,\)
\(\displaystyle \sin \color{red}\alpha=\frac{1}{2}\small,\)
Острый угол, синус которого \(\displaystyle \frac{1}{2}\small,\) равен \(\displaystyle 30^{\circ}{\small:}\)
\(\displaystyle \color{red}\alpha=30^\circ\small.\)
Ответ: \(\displaystyle 30^\circ\small.\)