В прямоугольном треугольнике \(\displaystyle ABC\) угол \(\displaystyle C\) прямой, \(\displaystyle \angle B= 56^{\circ}{\small,}\) \(\displaystyle CD\) – медиана.
Найдите угол \(\displaystyle ACD{\small.}\)
\(\displaystyle \angle ACD=\)\(\displaystyle ^{\circ}{\small.}\)
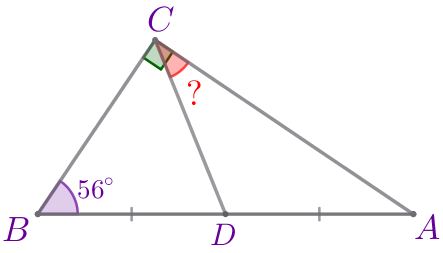 | \(\displaystyle ABC\) – прямоугольный треугольник:
Требуется найти угол \(\displaystyle ACD{\small.}\) |
| Медиана, проведённая к гипотенузе прямоугольного треугольника, равна половине гипотенузы. | 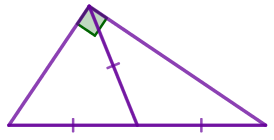 |
Согласно свойству прямоугольного треугольника
\(\displaystyle CD=BD=AD{\small.}\)
Следовательно,
\(\displaystyle \triangle CDB\) и \(\displaystyle \triangle CDA\) – равнобедренные треугольники.
В равнобедренном треугольнике углы при основании равны. Значит, в треугольнике \(\displaystyle CDB{\small:}\) \(\displaystyle \angle DCB=\angle DBC= 56^{\circ}{\small.}\) | 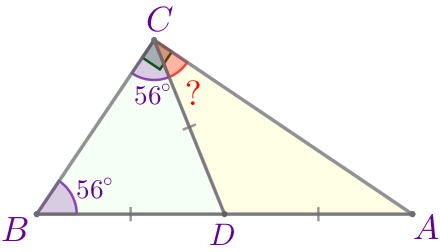 |
Угол \(\displaystyle C\) – прямой и равен сумме двух углов:
\(\displaystyle \angle C=\angle DCB+\angle ACD{\small;}\)
\(\displaystyle 90^{\circ}=56^{\circ}+\angle ACD{\small.}\)
Найдем угол \(\displaystyle ACD{\small:}\)
\(\displaystyle \angle ACD=90^{\circ}-56^{\circ}=34^{\circ}{\small.}\)
Ответ: \(\displaystyle \angle ACD=34^{\circ}{\small.}\)