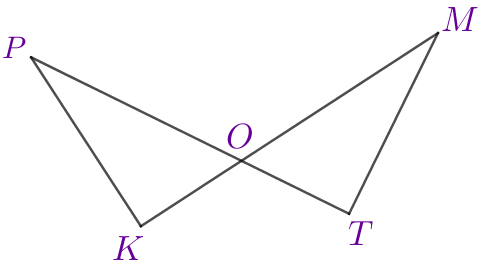
На рисунке \(\displaystyle PO=OM{\small,}\) \(\displaystyle \angle PKO=\angle MTO=90^{\circ}{\small.}\) Найдите длину отрезка \(\displaystyle MT{\small,}\) если \(\displaystyle PK=14{\small.}\)
\(\displaystyle MT=\)\(\displaystyle {\small.}\)
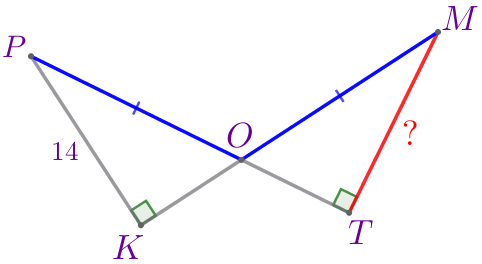 |
Требуется найти длину отрезка \(\displaystyle MT{\small.}\) |
Рассмотрим прямоугольные треугольники \(\displaystyle OPK\) и \(\displaystyle OMT{\small.}\)
 |
|
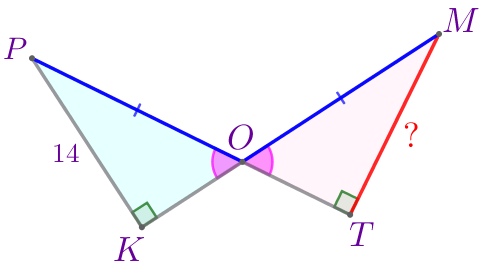
Следовательно,
\(\displaystyle \triangle OPK= \triangle OMT\)
по гипотенузе и острому углу.
В равных треугольниках напротив соответственно равных углов лежат равные стороны. Значит,
\(\displaystyle MT=PK=14{\small.}\)
Ответ: \(\displaystyle MT=14{\small.}\)