Один из углов прямоугольного треугольника равен \(\displaystyle 60^{\circ}{\small,}\) а разность гипотенузы и меньшего катета равна \(\displaystyle 8\, \footnotesize см{\small.}\) Найдите гипотенузу и меньший катет треугольника.
гипотенуза равна \(\displaystyle \footnotesize см{\small,}\)
меньший катет равен \(\displaystyle \footnotesize см{\small.}\)
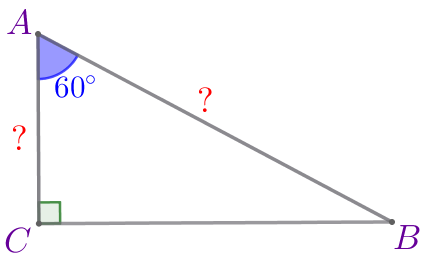
Пусть \(\displaystyle ABC\) – прямоугольный треугольник:
 |
|
Требуется найти гипотенузу и меньший катет, то есть \(\displaystyle AB\) и \(\displaystyle AC{\small.}\)
Поскольку сумма острых углов прямоугольного треугольника равна \(\displaystyle 90^{\circ}{\small,}\) то
\(\displaystyle \angle B=90^{\circ}-\angle A=90^{\circ}-60^{\circ}=30^{\circ}{\small.}\)
| В прямоугольном треугольнике напротив угла в \(\displaystyle 30^{\circ}\) лежит катет равный половине гипотенузы. | 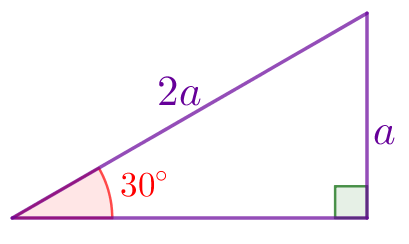 |
Пусть \(\displaystyle AC=\color{red}{x}{\small,}\) тогда \(\displaystyle AB=\color{red}{2x}{\small.}\) По условию \(\displaystyle AB-AC=8\,\footnotesize см{\small.}\) То есть \(\displaystyle \color{red}{2x}-\color{red}{x}=8\,\footnotesize см{\small;}\) \(\displaystyle \color{red}{x}=8\,\footnotesize см{\small.}\) | 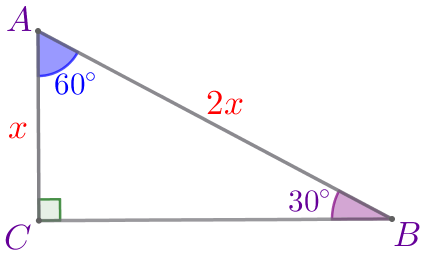 |
Значит,
\(\displaystyle AC=8\,\footnotesize см{\small,}\)
\(\displaystyle AB=2\cdot 8=16\,\footnotesize см{\small.}\)
| Ответ: | гипотенуза равна \(\displaystyle 16\,\footnotesize см{\small,}\) |
| меньший катет равен \(\displaystyle 8\,\footnotesize см{\small.}\) |