Медиана, проведенная к основанию равнобедренного треугольника, равна \(\displaystyle 5\small,\) а основание треугольника равно \(\displaystyle 6\small.\) Найдите две другие медианы треугольника.
Расположим треугольник так, чтобы
- начало координат совпадало с основанием медианы \(\displaystyle AM\small,\)
- основание \(\displaystyle BC\) лежало на оси \(\displaystyle Ox\small.\)
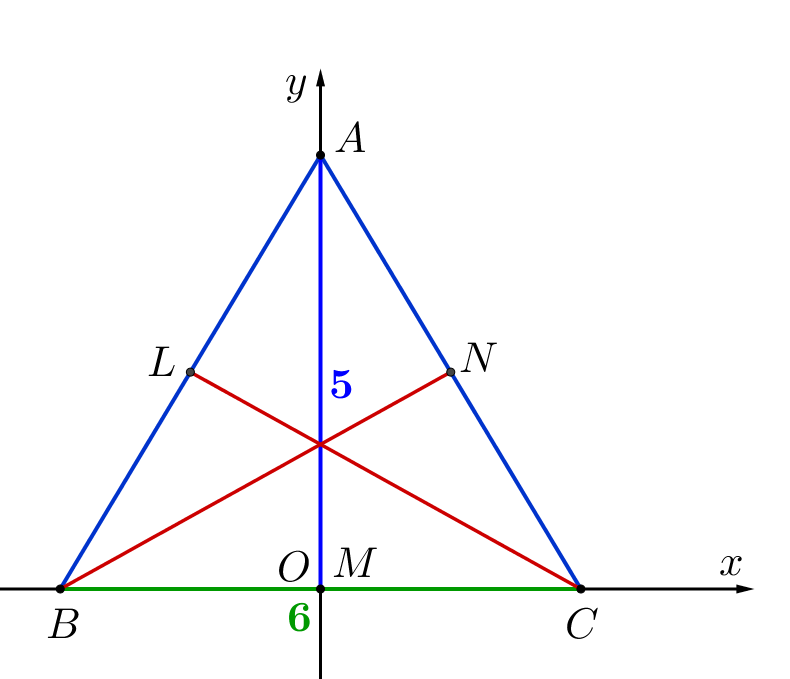
Найдите координаты точек \(\displaystyle A,\,B\) и \(\displaystyle C{\small:}\)
\(\displaystyle A\)( ; )
\(\displaystyle B\)( ; )
\(\displaystyle C\)( ; )
Зная координаты точек \(\displaystyle A,\,B\) и \(\displaystyle C{ \small ,}\) найдите медианы \(\displaystyle BN\) и \(\displaystyle CL{\small:}\)
Введем прямоугольную систему координат так, чтобы
- начало координат совпадало с основанием медианы \(\displaystyle AM\small,\)
- основание \(\displaystyle BC\) лежало на оси \(\displaystyle Ox\small.\)
Медиана делит основание треугольника пополам, то есть \(\displaystyle BM=CM=\frac{BC}{2}=\frac{6}{2}=3\small.\) Значит, координаты точек: \(\displaystyle B(-3;\,0)\) и \(\displaystyle C(3;\,0)\small.\) По условию, треугольник равнобедренный, откуда\(\displaystyle AB=AC\small.\) Тогда медиана \(\displaystyle AM\) является и высотой. То есть точка \(\displaystyle A\) лежит на оси \(\displaystyle Oy\) и ее координата: \(\displaystyle A(0;\,5)\small.\) | 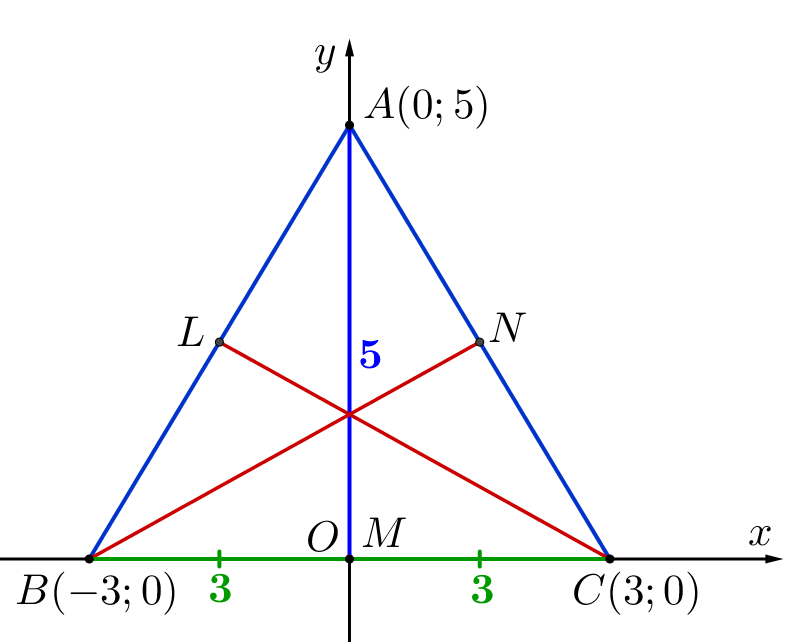 |
Зная координаты вершин треугольника, найдем длину его медиан.
\(\displaystyle BN=\frac{\sqrt{106}}{2}\)
Точка \(\displaystyle N\) – середина отрезка \(\displaystyle AC\small,\) тогда ее координаты
\(\displaystyle N\left(\frac{0+3}{2};\,\frac{5+0}{2}\right)=N\left(\frac{3}{2};\,\frac{5}{2}\right)\small.\)
Расстояние между точками
Расстояние между точками с координатами \(\displaystyle (x_1;\,y_1)\) и \(\displaystyle (x_2;\,y_2)\) равно
\(\displaystyle d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\small.\)
Координаты точек \(\displaystyle B(-3;\,0)\) и \(\displaystyle N\left(\frac{3}{2};\,\frac{5}{2}\right)\small.\) Тогда расстояние между \(\displaystyle B\) и \(\displaystyle N\) равно
\(\displaystyle BN=\sqrt{\left(-3-\frac{3}{2}\right)^2+\left(0-\frac{5}{2}\right)^2}=\frac{\sqrt{106}}{2}\small.\)
Поскольку треугольник равнобедренный, то медианы, проведенные к сторонам \(\displaystyle AC\) и \(\displaystyle AB{ \small ,}\) равны:
\(\displaystyle BN=CL=\frac{\sqrt{106}}{2}\small.\)
Ответ: \(\displaystyle \frac{\sqrt{106}}{2}\small.\)