Высота треугольника, равная \(\displaystyle 10\small,\) делит основание на отрезки \(\displaystyle 10\) и \(\displaystyle 4\small.\) Найдите медиану, проведенную к большей из двух других сторон.
Расстояние между точками
Расстояние между точками с координатами \(\displaystyle (x_1;\,y_1)\) и \(\displaystyle (x_2;\,y_2)\) равно
\(\displaystyle d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\small.\)
Чтобы решить задачу:
- введем прямоугольную систему координат;
- определим, какая из сторон треугольника больше;
- найдем длину медианы, проведенной к большей стороне.
1. Рассмотрим треугольник \(\displaystyle ABC\) и его высоту \(\displaystyle AH\small.\) Тогда \(\displaystyle AH=10,\,BH=10\) и \(\displaystyle CH=4\small.\)
Введем прямоугольную систему координат, как показано на рисунке:
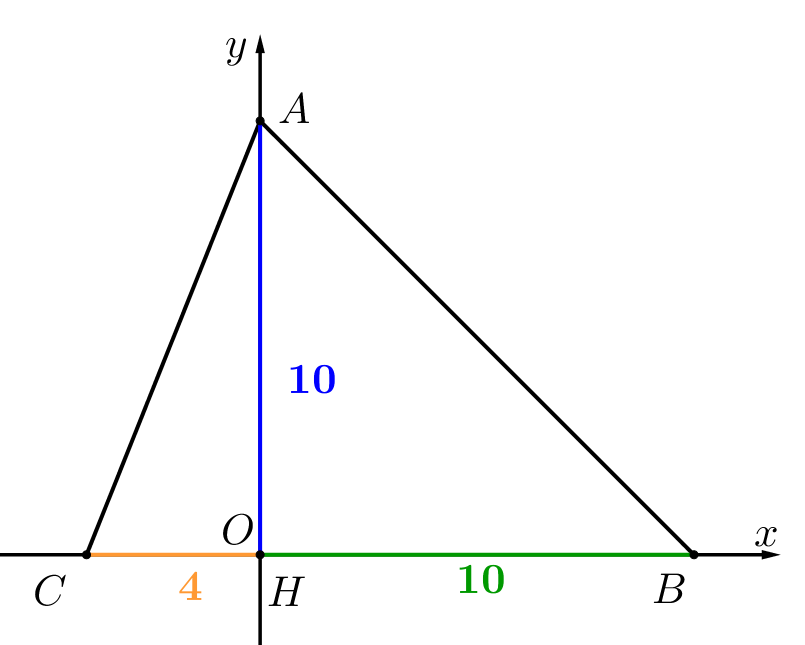
Тогда координаты точки \(\displaystyle H(0;\,0)\small,\) а координаты вершин треугольника:
\(\displaystyle A(0;\,10),\,B(10;\,0)\) и \(\displaystyle C(-4;\,0)\small.\)
2. Определим, какая из сторон \(\displaystyle AB\) и \(\displaystyle AC\) больше:
\(\displaystyle AB=\sqrt{(0-10)^2+(10-0)^2}=\sqrt{200}\small.\)
\(\displaystyle AC=\sqrt{(0-(-4))^2+(10-0)^2}=\sqrt{116}\small.\)
То есть \(\displaystyle AB>BC\small.\)
3. Найдем медиану, проведенную к \(\displaystyle AB\small.\)
Обозначим середину стороны \(\displaystyle AB\) за \(\displaystyle M\small.\) Тогда ее координата равна полусумме координат \(\displaystyle A\) и \(\displaystyle B{\small:}\) \(\displaystyle M\left(\frac{0+10}{2};\,\frac{10+0}{2}\right)=M\left(5;\,5\right)\small.\) Зная координаты \(\displaystyle C(-4;\,0)\) и \(\displaystyle M\left(5;\,5\right)\small,\) находим длину \(\displaystyle CM{\small:}\) \(\displaystyle CM=\sqrt{(-4-5)^2+(0-5)^2}=\sqrt{106}\small.\) | 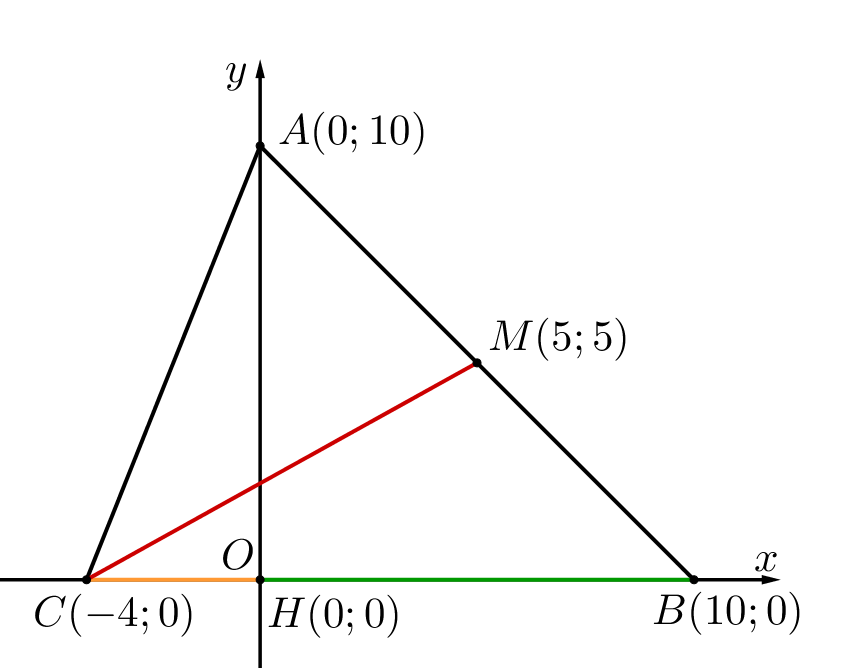 |
Ответ: \(\displaystyle \sqrt{106}\small.\)