В прямоугольнике \(\displaystyle ABCD\) сторона \(\displaystyle AB=8\) и \(\displaystyle AD=12\small.\) Точка \(\displaystyle M\) – середина \(\displaystyle AD\small,\) точка \(\displaystyle K\) – середина \(\displaystyle BM\small.\) Найдите длину отрезка \(\displaystyle CK\small.\)
Чтобы решить задачу, введем систему координат и последовательно вычислим координаты всех точек.
Введем прямоугольную систему координат так, чтобы:
| 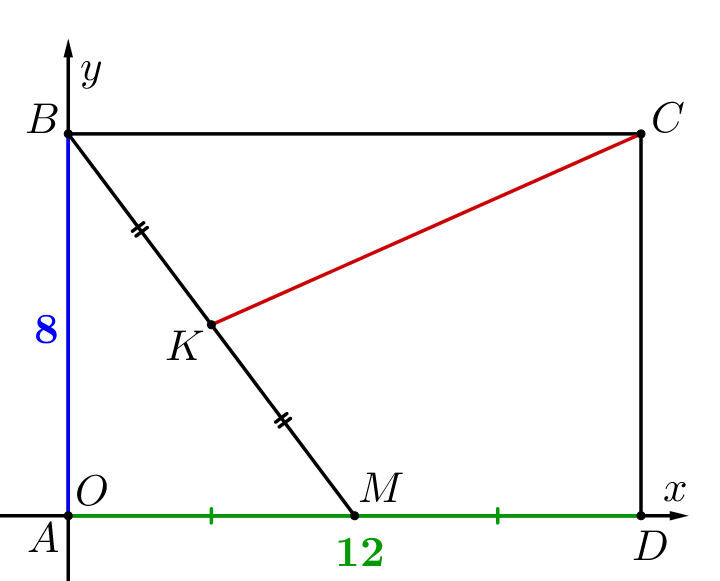 |
В такой системе координат координаты вершин прямоугольника:
\(\displaystyle A(0;\,0),\,B(0;\,8),\,C(12;\,8)\) и \(\displaystyle D(12;\,0)\small.\)
Точка \(\displaystyle M\) – середина стороны \(\displaystyle AD\small,\) тогда ее координата:
\(\displaystyle M(6;\,0)\small.\)
Точка \(\displaystyle K\) – середина отрезка \(\displaystyle BM\small.\) Тогда ее координаты – полусумма координат концов:
\(\displaystyle K\left(\frac{0+6}{2};\,\frac{8+0}{2}\right)=K\left(3;\,4\right)\small.\)
Теперь, зная координаты точек \(\displaystyle C\) и \(\displaystyle K\small,\) найдем длину отрезка \(\displaystyle CK\small.\)
Расстояние между точками
Расстояние между точками с координатами \(\displaystyle (x_1;\,y_1)\) и \(\displaystyle (x_2;\,y_2)\) равно
\(\displaystyle d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\small.\)
Координаты точек: \(\displaystyle C(12;\,8)\) и \(\displaystyle K\left(3;\,4\right)\small,\) тогда
\(\displaystyle CK=\sqrt{(12-3)^2+(8-4)^2}=\sqrt{97}\small.\)
Ответ: \(\displaystyle CK=\sqrt{97}\small.\)