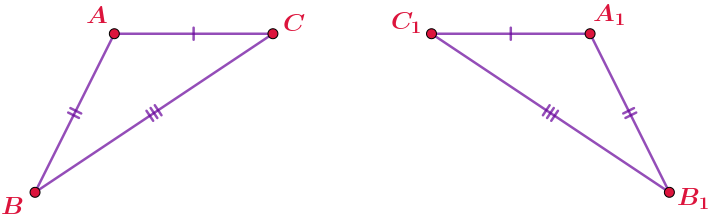
Четырёхугольник \(\displaystyle ABCD\) имеет две пары равных сторон, отмеченные на рисунке.
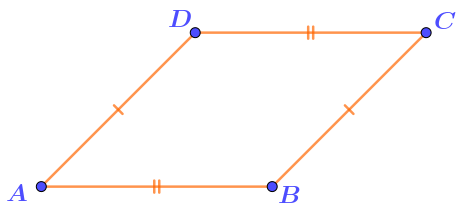
Дополните доказательство равенства углов \(\displaystyle ABC\) и \(\displaystyle ADC{\small .}\)
Проведём отрезок \(\displaystyle AC\) и рассмотрим треугольники \(\displaystyle ABC\) и \(\displaystyle ADC{\small .}\)
| \(\displaystyle \left\{ \begin{array}{ll} \\ \\\\\\ \\\\ \end{array} \right.\) | |||||
| \(\displaystyle {\LARGE\Rightarrow}\) | \(\displaystyle {\LARGE\Rightarrow}\) | \(\displaystyle \angle ABC=\angle ADC\) | |||
\(\displaystyle {\footnotesize \it (по~третьему}\) \(\displaystyle {\footnotesize \it признаку)}\) |
Равенство углов можно получить из равенства треугольников.
Проведённый отрезок \(\displaystyle AC\) является общей стороной двух треугольников. Элементами этих треугольников как раз являются углы, равенство которых доказывается.
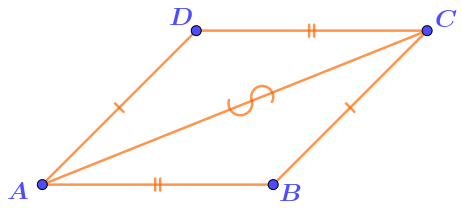
Записать доказательство равенства треугольников можно так:
\(\displaystyle\left\{\begin{array}{}AD=BC\\AB=DC\\AC - {\footnotesize \it общая~сторона}\end{array} {\LARGE\Rightarrow} \quad {\bf\triangle}ABC={\bf\triangle}CDA ~~{\footnotesize \it (по~третьему~признаку)}\right.\)
Напротив общей стороны равных треугольников расположены равные углы.
Значит, \(\displaystyle \angle ABC=\angle ADC{\small .}\)
| Ответ: |  |