На отрезке \(\displaystyle AB\) взята точка \(\displaystyle K{\small ,}\) а вне прямой \(\displaystyle AB\) точки \(\displaystyle P\) и \(\displaystyle Q{\small .}\)
Оказалось, что:
- расстояния от точки \(\displaystyle K\) до точек \(\displaystyle A\) и \(\displaystyle P\) соответственно равны расстояниям от точки \(\displaystyle Q\) до точек \(\displaystyle K\) и \(\displaystyle B{\text ;}\)
- сумма расстояний от точки \(\displaystyle K\) до точек \(\displaystyle B\) и \(\displaystyle Q\) равна сумме расстояний от точки \(\displaystyle A\) до точек \(\displaystyle K\) и \(\displaystyle P{\small .}\)
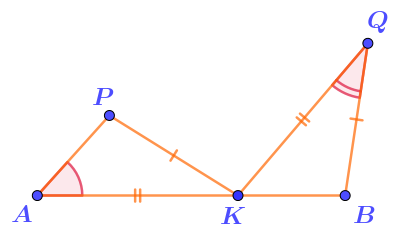
Известны два угла: \(\displaystyle \angle PAK=48\degree \) и \(\displaystyle \angle BQK=32\degree{\small .}\)
Найти величину угла \(\displaystyle PKQ{\small .}\)
\(\displaystyle \angle PKQ=\)\(\displaystyle \degree \)
Сумма расстояний от точки \(\displaystyle K\) до точек \(\displaystyle B\) и \(\displaystyle Q\) равна сумме расстояний от точки \(\displaystyle A\) до точек \(\displaystyle K\) и \(\displaystyle P{\text :}\)
\(\displaystyle KB+KQ=AK+AP{\small .}\)
Расстояния между точками являются также длинами отрезков с концами в этих точках. Отрезки \(\displaystyle AK\) и \(\displaystyle KQ\) по условию равны.
Убирая равные слагаемые из двух частей равенства сумм, получаем \(\displaystyle KB=AP{\small .}\) Отметим на рисунке равные отрезки.
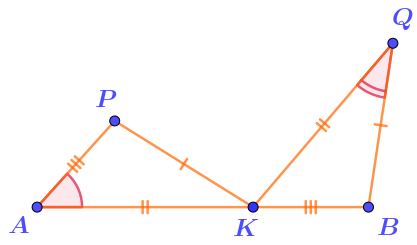
\(\displaystyle\left\{\begin{array}{}KP=QB\\AK=KQ\\KB=AP\end{array}\quad{\LARGE\Rightarrow} \quad\begin{array}{} \\{\bf\triangle}AKP={\bf\triangle}KQB \\{\footnotesize\it (по~третьему~признаку)}\end{array}\right.\)
Отметим в равных треугольниках равные углы, расположенные против равных сторон:
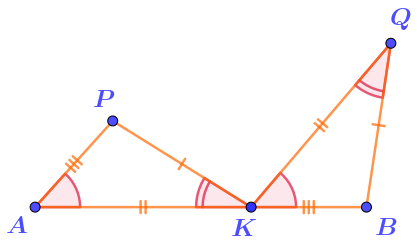
\(\displaystyle \angle BKQ=\angle PAK=48\degree {\small ,\;}\angle AKP=\angle BQK=32\degree {\small .}\)
Развёрнутый угол \(\displaystyle AKB\) имеет величину \(\displaystyle 180\degree \) и составлен из частей \(\displaystyle AKP{\small ,\;}BKQ\) и \(\displaystyle PKQ{\small .}\)
Величину неизвестной части выразим через величины известных частей:
\(\displaystyle \angle PKQ=180\degree - \angle AKP -\angle BKQ=180\degree -32\degree -48\degree=100\degree {\small .}\)
Ответ: \(\displaystyle \angle PKQ=100\degree \)