В треугольнике \(\displaystyle AMN\) известны два угла: \(\displaystyle \angle AMN=47\degree {\small ,\;}\angle ANM=28\degree {\small .}\)
Расстояния от точки \(\displaystyle B\) до его вершин \(\displaystyle M\) и \(\displaystyle N\) соответственно равны длинам сторон \(\displaystyle AN\) и \(\displaystyle AM{\small .}\)
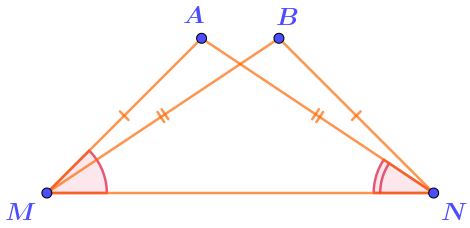
Найдите величину угла \(\displaystyle ANB{\small .}\)
\(\displaystyle \angle ANB=\)\(\displaystyle \degree \)
Искомый угол \(\displaystyle ANB\) вместе с известным по условию углом \(\displaystyle ANM\) составляют угол \(\displaystyle BNM{\small .}\)
Величину угла \(\displaystyle BNM\) можно установить, если найти равный ему известный угол. Найдём равные треугольники, элементом одного из которых являетсяугол \(\displaystyle BNM{\small .}\)
Выпишем равные элементы треугольников \(\displaystyle AMN\) и \(\displaystyle BNM{\small ,}\) дополнив обозначения рисунка их общей стороной \(\displaystyle MN{\text :}\)
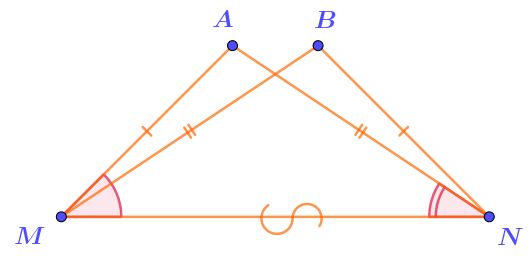
\(\displaystyle\left\{\begin{array}{}AM=BN\\AN=BM\\MN-{\footnotesize \it общая~сторона}\end{array} {\LARGE\Rightarrow} \quad {\bf\triangle}AMN={\bf\triangle}BNM~{\footnotesize \it (по~третьему~признаку)}\right.\)
В равных треугольниках напротив равных сторон \(\displaystyle AN\) и \(\displaystyle BM\) расположены равные углы:
\(\displaystyle \angle BNM=\angle AMN=47\degree {\small .}\)
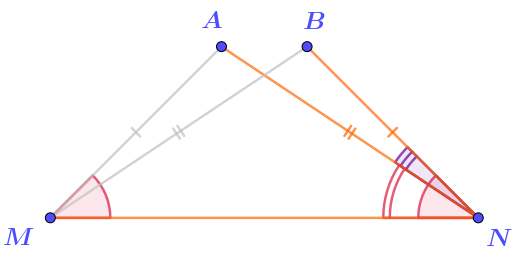
\(\displaystyle \angle ANB=\angle BNM-\angle ANM=47\degree -28\degree =19\degree {\small .}\)
Ответ: \(\displaystyle \angle ANB=19\degree {\small .}\)