Соберите три пары треугольников, равенство которых доказывается по разным признакам.
\(\displaystyle =\)
| ||||
| \(\displaystyle =\) | \(\displaystyle ({\rm III}~{\footnotesize признак})\) | |||
\(\displaystyle =\)
| По стороне и двум прилежащим к ней углам |
Будем последовательно снизу вверх заполнять строки таблицы.
Требование к составу пар равных элементов прямо указано в таблице. Этот состав соответствует второму признаку равенства треугольников. Сразу вносим эту информацию в таблицу.
Среди вариантов ответа есть четыре треугольника, в которых отмечено по два угла.
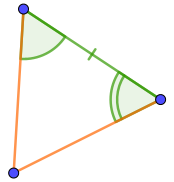
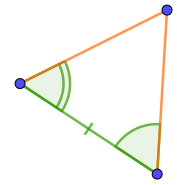
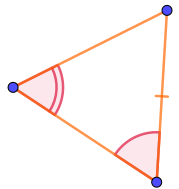
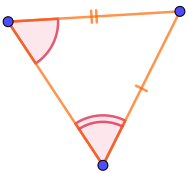
Из этих четырёх треугольников только у первых двух попарно равные углы прилежат к отмеченным как равные сторонам. Второй признак равенства треугольников требует именно этого.
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то треугольники равны.
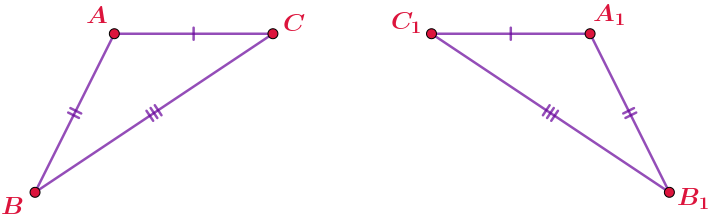
\(\displaystyle\left\{\begin{array}{}AC=A_1C_1\\AB=A_1B_1\\BC=B_1C_1\end{array} {\LARGE\Rightarrow} \quad {\bf\triangle}ABC={\bf\triangle}A_1B_1C_1\right.\)
С тремя отметками на сторонах среди вариантов ответа находим только два треугольника.
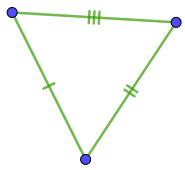
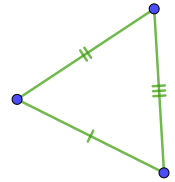
Внесём номер признака (первый) и соответствующее ему описание (по двум сторонам и углу между ними) в таблицу.
Рассмотрим оставшиеся пять треугольников.
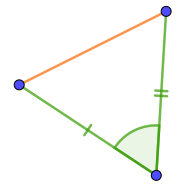
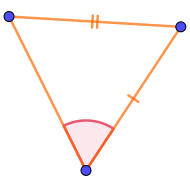
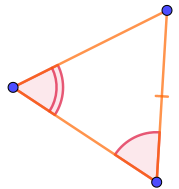
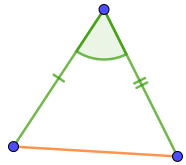
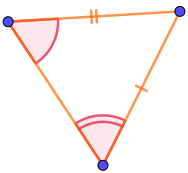
Только в двух из треугольников отмеченный угол заключён между двумя отмеченными сторонами.
И эти два треугольника действительно имеют требуемый первым признаком набор равных элементов.
| Ответ: | 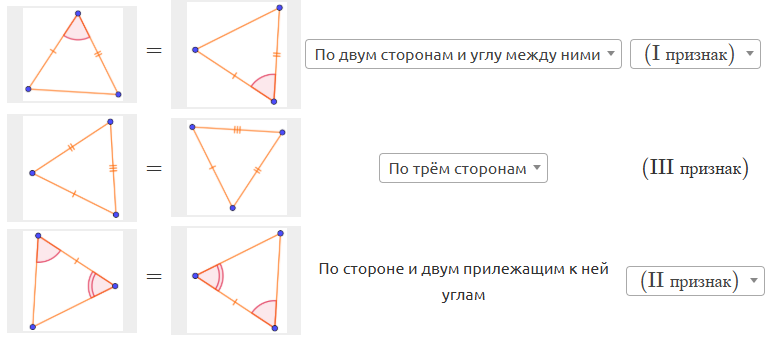 |