Даны две точки \(\displaystyle A\) и \(\displaystyle B\small.\) Найдите множество всех точек \(\displaystyle M\small,\) для каждой из которых
\(\displaystyle BM^2-AM^2=\frac{1}{2}AB^2\small.\)
Выберите верный ответ из списка:
Обозначим длину отрезка \(\displaystyle AB=b\small.\)
Введем прямоугольную систему координат так, что:
- точка \(\displaystyle A\) – начало координат;
- отрезок \(\displaystyle AB\) лежит на оси абсцисс.
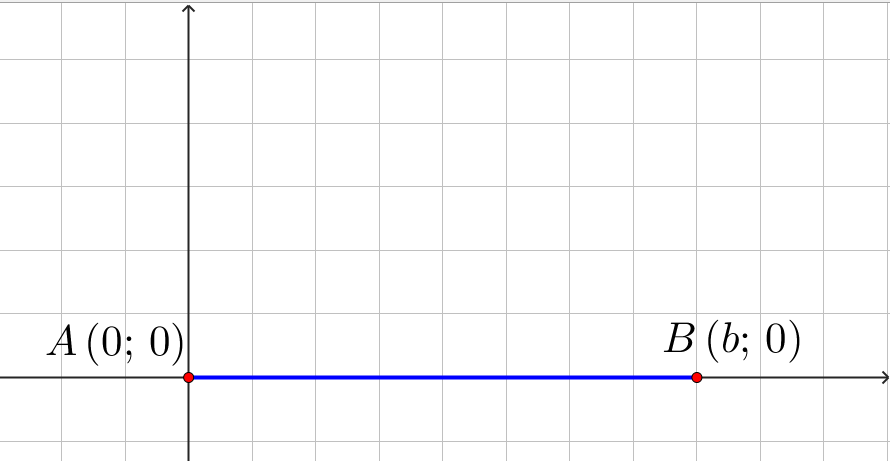
Тогда точки \(\displaystyle A\) и \(\displaystyle B\) будут иметь координаты: \(\displaystyle A(0;\,0),\,B(b;\,0)\small.\)
Пусть точка \(\displaystyle M \) имеет координаты \(\displaystyle (x;\,y)\small.\)
- \(\displaystyle AM^2=x^2+y^2\small,\)
- \(\displaystyle BM^2=(x-b)^2+y^2\small,\)
- \(\displaystyle AB^2=b^2\small.\)
Подставляя в выражение \(\displaystyle BM^2-AM^2=\frac{1}{2}AB^2\small,\) предложенное в условии, получаем:
\(\displaystyle (x-b)^2+\cancel{y^2}-(x^2+\cancel{y^2})=\frac{1}{2}b^2\small.\)
Приведем подобные слагаемые, получаем:
\(\displaystyle (x-b)^2-x^2=\frac{1}{2}b^2\small.\)
\(\displaystyle x=\frac{1}{4}b\small.\)
Таким образом, все точки \(\displaystyle M\) из условия лежат на прямой, заданной уравнением
\(\displaystyle x=\frac{1}{4}b\small.\)
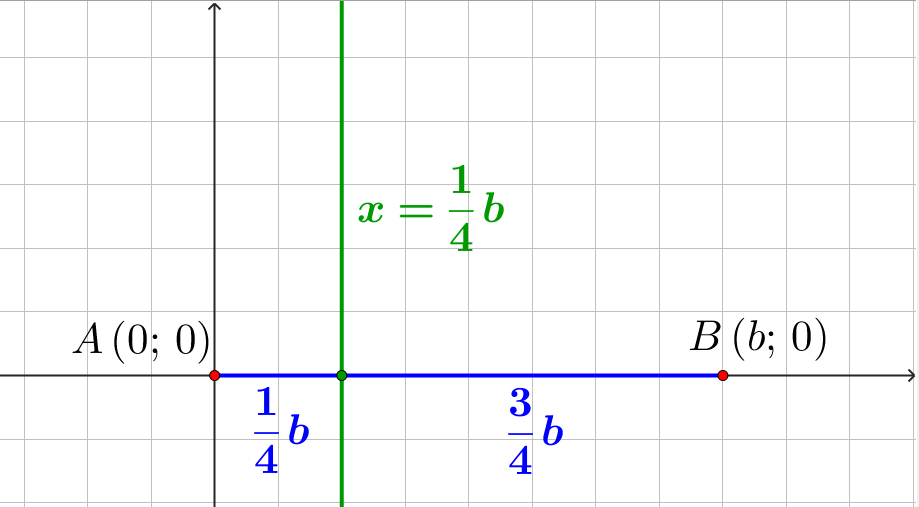
Эта прямая перпендикулярна отрезку \(\displaystyle AB\) и делит его в отношении \(\displaystyle 1:3\small.\)