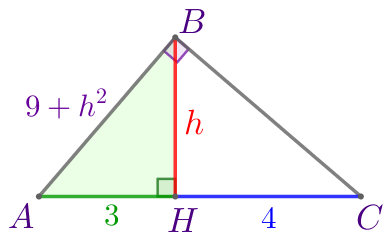
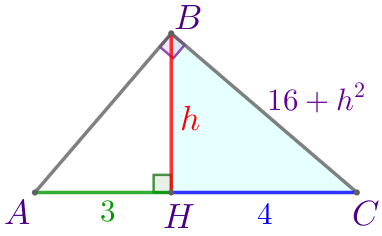
Высота прямоугольного треугольника делит гипотенузу на отрезки \(\displaystyle 3\) и \(\displaystyle 4\small.\) Найдите эту высоту.
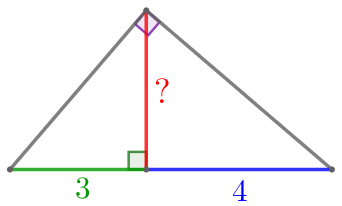
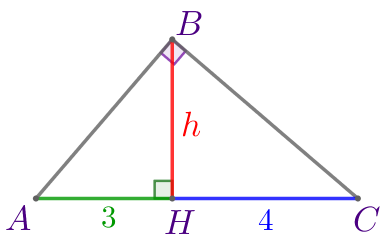
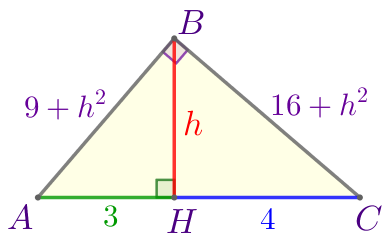
Обозначим вершины треугольника и основание высоты буквами \(\displaystyle A{\small,}\) \(\displaystyle B{\small,}\) \(\displaystyle C\) и \(\displaystyle H\) соответственно.
 |
Требуется найти \(\displaystyle \color{red}{h}{\small.}\) |
\(\displaystyle AB^2=9+\color{red}{h}^2{\small.}\)
\(\displaystyle BC^2=16+\color{red}{h}^2{\small.}\)
\(\displaystyle AC^2=AB^2+BC^2{\small.}\)
 |
Подставляя, получаем: \(\displaystyle 7^2=(9+\color{red}{h}^2)+(16+\color{red}{h}^2){\small.}\) |
Упростим выражение и найдем \(\displaystyle \color{red}{h}{\small:}\)
\(\displaystyle 7^2=25+2\color{red}{h}^2{\small;}\)
\(\displaystyle 2\color{red}{h}^2=49-25{\small;}\)
\(\displaystyle 2\color{red}{h}^2=24{\small;}\)
\(\displaystyle \color{red}{h}^2=12{\small.}\)
Так как длина высоты неотрицательна, то
\(\displaystyle \color{red}{h}=\sqrt{12}=2\sqrt{3}\small.\)
Ответ: \(\displaystyle 2\sqrt{3}\small.\)