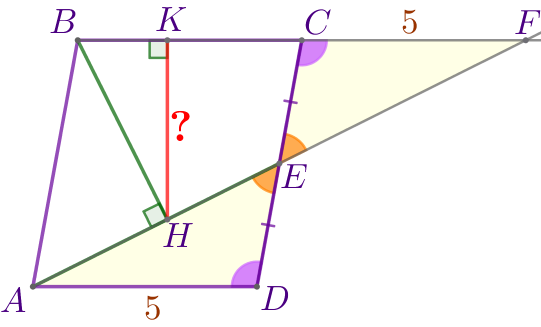
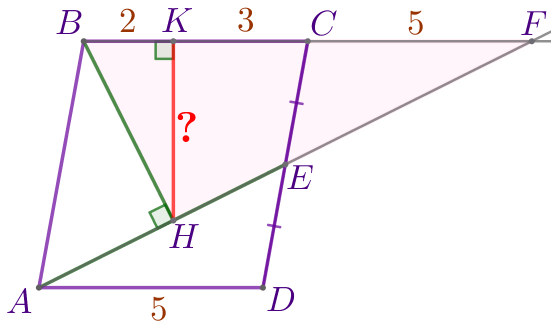
Теория: 09 Среднее геометрическое-2

Задание

Точка \(\displaystyle E\) – середина стороны \(\displaystyle CD\) параллелограмма \(\displaystyle ABCD{\small.}\) На отрезок \(\displaystyle AE\) опустили перпендикуляр \(\displaystyle BH{\small.}\) На сторону \(\displaystyle BC\) опустили перпендикуляр \(\displaystyle HK{\small.}\) Найдите \(\displaystyle HK{\small,}\) если \(\displaystyle BK=2{\small,}\) \(\displaystyle CK=3{\small.}\)

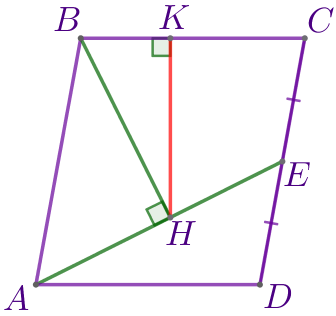
\(\displaystyle HK=\)

Решение

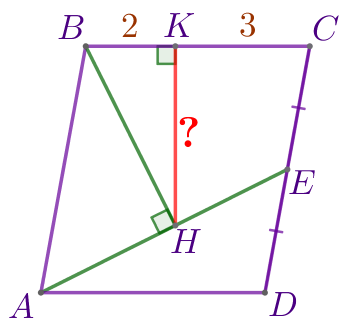\(\displaystyle ABCD\) – параллелограмм:

\(\displaystyle E \in CD{\small,} \) \(\displaystyle CE=ED{\small;}\)
\(\displaystyle H \in AE{\small,} \) \(\displaystyle BH \perp AE{\small;}\)
\(\displaystyle K \in BC{\small,} \) \(\displaystyle HK \perp BC{\small;}\)
\(\displaystyle BK=2{\small,}\) \(\displaystyle KC=3{\small.}\)

Требуется найти длину отрезка \(\displaystyle HK{\small.}\)

Заметим, что:

Точка \(\displaystyle K\) лежит на отрезке \(\displaystyle BC{\small,}\) значит,

\(\displaystyle BC=BK+KC=2+3=5{\small.}\)

Противоположные стороны параллелограмма параллельны и равны, значит,

\(\displaystyle AD \parallel BC\) и \(\displaystyle AD=BC=5{\small.}\)

Выполним дополнительное построение.

Продлим отрезок \(\displaystyle AE\) за точку \(\displaystyle E\) до пересечения с прямой \(\displaystyle BC{\small.}\)

Точку пересечения обозначим буквой \(\displaystyle F{\small.}\)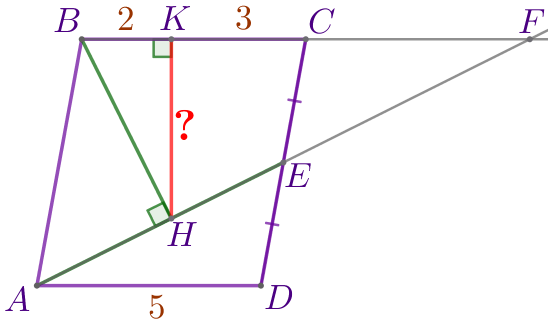

\(\displaystyle CF=AD=5{\small.}\)

Рассмотрим прямоугольный треугольник \(\displaystyle FBH{\small.}\)

\(\displaystyle HK\) – высота, проведенная к гипотенузе;

\(\displaystyle BK=2{\small;}\)

\(\displaystyle KF=KC+CF=3+5=8{\small.}\)

Воспользуемся правилом:

Правило

Высота в прямоугольном треугольнике равна среднему геометрическому отрезков, на которые она делит гипотенузу.

То есть

\(\displaystyle HK=\sqrt{BK \cdot KF}=\sqrt{2 \cdot 8}=\sqrt{16}=4{\small.}\)

Ответ: \(\displaystyle HK=4{\small.}\)