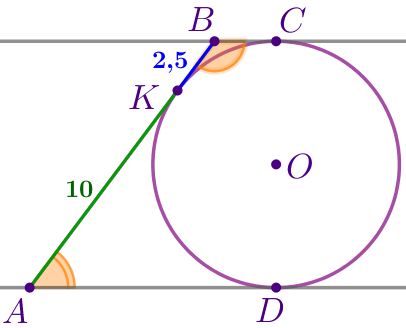
Окружность касается двух параллельных прямых и секущей, причем точка касания делит секущую на два отрезка длинами \(\displaystyle 2{,}5\) и \(\displaystyle 10{\small.}\) Найдите радиус окружности.
Пусть \(\displaystyle O\) – центр окружности.
Все точки, изображенные на рисунке, обозначим буквами.
 |
Требуется найти радиус окружности. |
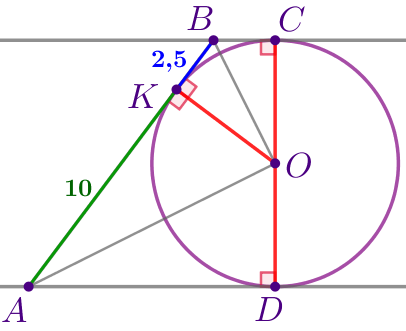 | Соединим отрезками центр окружности \(\displaystyle O\) с точками \(\displaystyle A{\small,}\) \(\displaystyle B{\small,}\) \(\displaystyle C{\small,}\) \(\displaystyle D{\small,}\) \(\displaystyle K{\small.}\) Заметим, что: \(\displaystyle OC=OD=OK\) – радиусы данной окружности. |
Радиус, проведённый в точку касания, перпендикулярен касательной. Значит,
\(\displaystyle OC \perp BC{\small;}\) \(\displaystyle OD \perp AD{\small;}\) \(\displaystyle OK \perp AB{\small.}\)
Рассмотрим две пары прямоугольных треугольников:
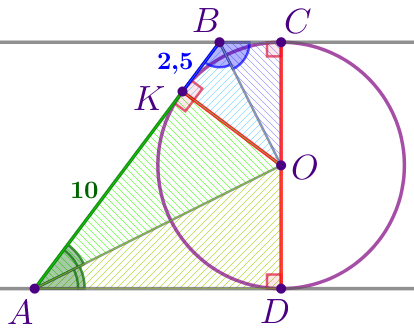 |
\(\displaystyle \angle OBK=\angle OBC{\small.} \)
\(\displaystyle \angle OAK=\angle OAD{\small.} \) |
Значит,
\(\displaystyle \angle ABO=\frac{1}{2}\angle ABC{\small,}\) \(\displaystyle \angle BAO=\frac{1}{2}\angle BAD{\small.}\)
\(\displaystyle \angle ABC+\angle BAD=180^{\circ}{\small.}\)
Тогда
\(\displaystyle \angle ABO+\angle BAO=\frac{1}{2}\left(\angle ABC+\angle BAD\right)=\frac{1}{2} \cdot 180^{\circ}=90^{\circ}{\small.}\)
Рассмотрим треугольник \(\displaystyle AOB{\small:}\)
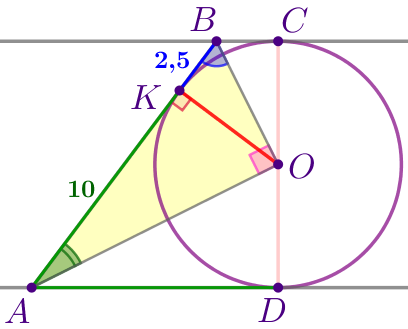 | Сумма внутренних углов треугольника равна \(\displaystyle 180^{\circ}{\small.}\) Тогда \(\displaystyle \angle AOB=180^{\circ}-(\angle ABO+\angle BAO){\small;}\) \(\displaystyle \angle AOB=180^{\circ}-90^{\circ}=90^{\circ}{\small.}\) Значит, треугольник \(\displaystyle AOB\) прямоугольный. |
Воспользуемся правилом:
Высота в прямоугольном треугольнике равна среднему геометрическому отрезков, на которые она делит гипотенузу.
То есть
\(\displaystyle OK=\sqrt{BK \cdot AK}=\sqrt{2{,5} \cdot 10}=\sqrt{25}=5{\small.}\)
Радиус окружности равен \(\displaystyle 5{\small.}\)
Ответ: \(\displaystyle 5{\small.}\)