В треугольнике \(\displaystyle FBE\) угол \(\displaystyle B\) прямой, \(\displaystyle FB=9,\) \(\displaystyle BE=12.\) Найдите длину вектора \(\displaystyle \overrightarrow {FB}+\overrightarrow {BE}.\)
Изобразим данный треугольник и указанные в условии векторы.
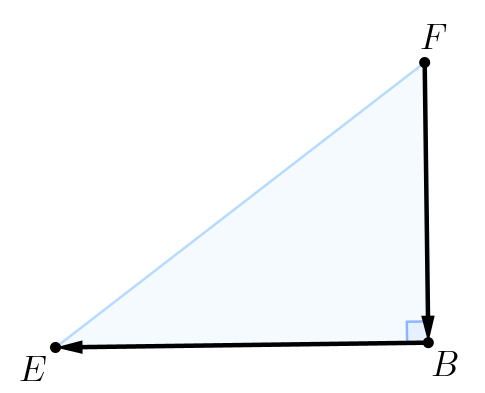
По правилу треугольника
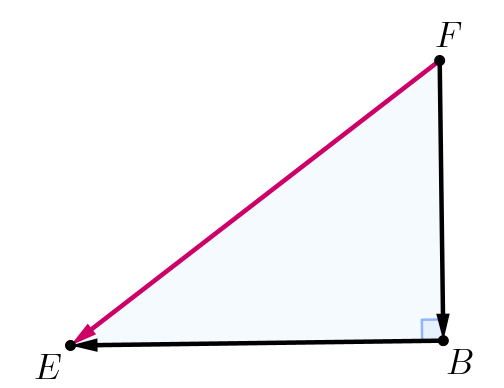
\(\displaystyle \overrightarrow {FB}+\overrightarrow {BE}=\color{#CC0066}{\overrightarrow {FE}}.\)
Длина вектора \(\displaystyle \color{#CC0066}{\overrightarrow {FE}}\) равна длине отрезка \(\displaystyle FE.\)
По теореме Пифагора из прямоугольного треугольника \(\displaystyle FBE\)
\(\displaystyle FE^2=FB^2+BE^2.\)
Значит,
\(\displaystyle FE^2=9^2+12^2=81+144=225=15^2,\)
\(\displaystyle FE=15.\)
Следовательно, \(\displaystyle |\overrightarrow {FE}|=FE=15.\)
Ответ: \(\displaystyle 15.\)