На рисунке изображена фигура (все углы прямые). Длины отрезков указаны в сантиметрах.
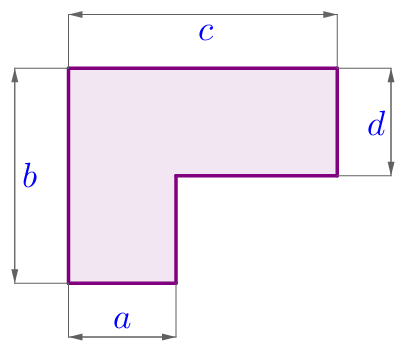
Периметр данной фигуры можно вычислить по формуле
При \(\displaystyle a=2\ {\small см,}\) \(\displaystyle b=8\ {\small см,}\) \(\displaystyle c=6\ {\small см,}\) \(\displaystyle d=3\ {\small см}\)
периметр этой фигуры равен \(\displaystyle {\small см}.\)
Периметр многоугольника равен сумме длин всех его сторон.
\(\displaystyle \color{red}{1)} \) Составим формулу для вычисления периметра данной фигуры.
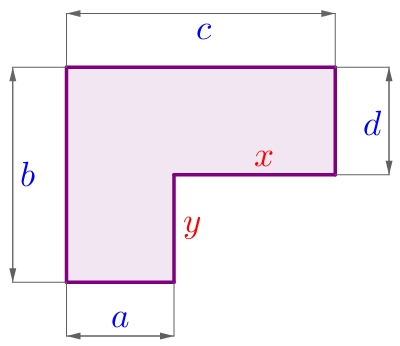 | На исходном рисунке указаны длины четырёх сторон \(\displaystyle a{\small,}\) \(\displaystyle b{\small,}\) \(\displaystyle c{\small,}\) \(\displaystyle d\) данного шестиугольника. Пусть \(\displaystyle x\) и \(\displaystyle y\) – длины оставшихся двух сторон. Тогда периметр \(\displaystyle P\) шестиугольника равен \(\displaystyle P=a+b+c+d+x+y{\small.}\) |
Выполним дополнительное построение.
Продлим отрезки длиной \(\displaystyle a\) и \(\displaystyle d\) до пересечения. Так как все углы прямые, то получившийся жёлтый четырёхугольник является прямоугольником. В прямоугольнике противоположные стороны равны. Обозначим на рисунке равные стороны соответствующими буквами \(\displaystyle x\) и \(\displaystyle y{\small.}\) | 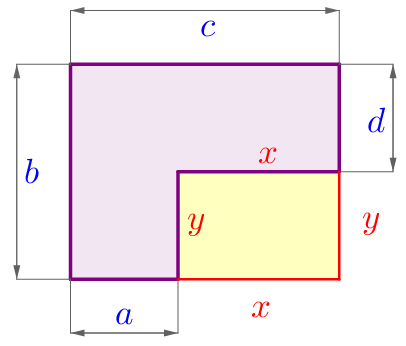 |
По рисунку видим, что \(\displaystyle \color{blue}{a}+\color{red}{x}=\color{blue}{c}\) и \(\displaystyle \color{blue}{d}+\color{red}{y}=\color{blue}{b}\) – как противоположные стороны прямоугольника.
Тогда
\(\displaystyle\begin{aligned}P&=\color{blue}{a}+b+c+\color{blue}{d}+\color{red}{x}+\color{red}{y}=\\&=\color{pink}{\underbrace{\color{blue}{a}\color{black}{+}\color{red}{x}}}+b+c+\color{pink}{\underbrace{\color{blue}{d}\color{black}{+}\color{red}{y}}}=\\&\kern{2em}=\color{blue}{c}+b+c+\color{blue}{b}=\\&\kern{3em}=2b+2c{\small.}\end{aligned}\)
То есть периметр данной фигуры можно вычислить по формуле \(\displaystyle 2b+2c{\small.}\)
\(\displaystyle \color{red}{2)} \) Найдем периметр данной фигуры при \(\displaystyle a=2\ {\small см,}\) \(\displaystyle b=8\ {\small см,}\) \(\displaystyle c=6\ {\small см,}\) \(\displaystyle d=3\ {\small см.}\)
\(\displaystyle P=2b+2c=2\cdot 8+2 \cdot 6=2\cdot (8+6)=2 \cdot 14=28{\small.}\)
| Ответ: | \(\displaystyle 2b+2c{\small,}\) |
| \(\displaystyle 28{\ \small см.}\) |