Диагонали \(\displaystyle AC\) и \(\displaystyle BD\) прямоугольника \(\displaystyle ABCD\) пересекаются в точке \(\displaystyle O{\small,}\) угол \(\displaystyle ABD\) больше угла \(\displaystyle CBD\) на \(\displaystyle 20^{\circ}{\small.}\) Найдите углы треугольника \(\displaystyle AOD{\small.}\)
\(\displaystyle \angle AOD=\) \(\displaystyle ^{\circ}{\small,}\) \(\displaystyle \angle OAD=\) \(\displaystyle ^{\circ}{\small,}\) \(\displaystyle \angle ODA=\) \(\displaystyle ^{\circ}{\small.}\)
\(\displaystyle O\) – точка пересечения диагоналей. Пусть \(\displaystyle \angle CBD=\color{blue}{\alpha}{\small.}\) Тогда по условию \(\displaystyle \angle ABD=\color{blue}{\alpha}+20^{\circ}{\small.}\) | 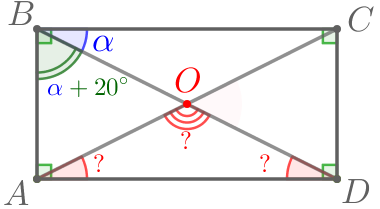 |
Требуется найти углы треугольника \(\displaystyle AOD{\small.}\)
В прямоугольнике \(\displaystyle ABCD{\small:}\)
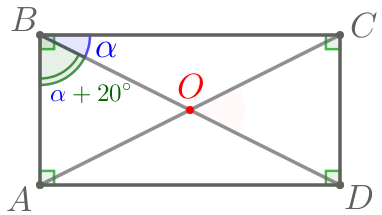 | \(\displaystyle \color{green}{\angle ABD}+\color{blue}{\angle CBD}=\angle ABC{\small.}\) Подставим
|
Получаем
\(\displaystyle \color{blue}{\alpha}+20^{\circ}+\color{blue}{\alpha}=90^{\circ}{\small.}\)
Решим уравнение и найдём \(\displaystyle \color{blue}{\alpha}{\small:}\)
\(\displaystyle 2 \cdot \color{blue}{\alpha}=70{\small;}\)
\(\displaystyle \color{blue}{\alpha}=35{\small.}\)
В прямоугольнике противоположные стороны попарно параллельны.
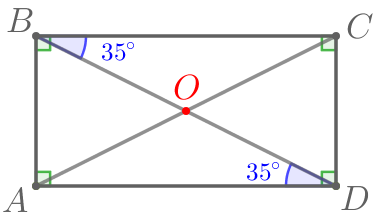 | Тогда \(\displaystyle \angle BDA=\angle CBD\) как накрест лежащие углы при параллельных прямых \(\displaystyle AD\) и \(\displaystyle BC\) и секущей \(\displaystyle BD{\small.}\) То есть \(\displaystyle \angle ODA=35^{\circ}{\small.}\) |
| Диагонали прямоугольника равны и точкой пересечения делятся пополам. | 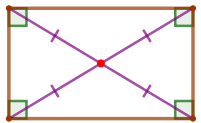 |
По свойству прямоугольника
\(\displaystyle OA=OD{\small.}\)
Следовательно, треугольник \(\displaystyle AOD\) – равнобедренный.
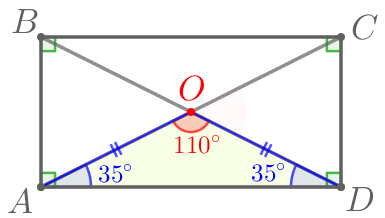 |
\(\displaystyle \angle OAD=\angle ODA=35^{\circ}{\small.}\)
\(\displaystyle \angle AOD=180^{\circ}-(\angle OAD+\angle ODA){\small.}\) |
\(\displaystyle \angle AOD=180^{\circ}-(35^{\circ}+35^{\circ})=180^{\circ}-70^{\circ}=110^{\circ}{\small.}\)
Ответ: \(\displaystyle \angle AOD=110^{\circ}{\small,}\) \(\displaystyle \angle OAD=35^{\circ}{\small,}\) \(\displaystyle \angle ODA=35^{\circ}{\small.}\)
