В прямоугольнике \(\displaystyle ABCD\) \(\displaystyle AB<BC{\small,}\) биссектриса угла \(\displaystyle A\) образует с диагональю \(\displaystyle BD\) углы, один из которых равен \(\displaystyle 105^{\circ}{\small.}\) Найдите меньший угол между диагоналями данного прямоугольника.
\(\displaystyle ^{\circ}{\small.}\)
По условию задачи выполним построение.
| 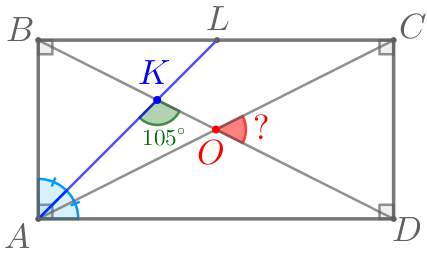 |
Требуется найти меньший угол между диагоналями данного прямоугольника, то есть угол \(\displaystyle COD{\small.}\)
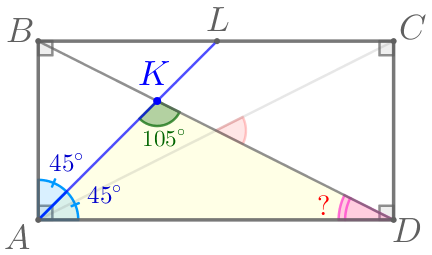
Рассмотрим треугольник \(\displaystyle AKD{\small.}\)
 |
|
Сумма внутренних углов треугольника равна \(\displaystyle 180^{\circ}{\small.}\)
Тогда
\(\displaystyle \angle ADK=180^{\circ}-(\angle AKD+\angle DAK){\small;}\)
\(\displaystyle \angle ADK=180^{\circ}-(105^{\circ}+45^{\circ})=180^{\circ}-150^{\circ}=30^{\circ}{\small.}\)
Диагонали прямоугольника равны и точкой пересечения делятся пополам. 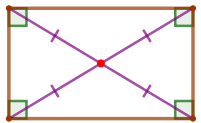
По свойству прямоугольника
\(\displaystyle OA=OD{\small.}\)
Рассмотрим равнобедренный треугольник \(\displaystyle AOD{\small.}\)
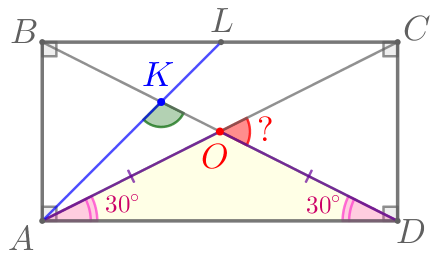 | В равнобедренном треугольнике углы при основании равны. Значит, \(\displaystyle \angle OAD=\angle ODA=30^{\circ}{\small.}\) |
Теорема о внешнем угле треугольника
| Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним. | 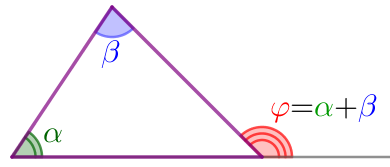 |
\(\displaystyle \angle COD\) – внешний угол треугольникa \(\displaystyle AOD{\small.}\) Следовательно,
\(\displaystyle \angle COD=\angle OAD+\angle ODA{\small;}\)
\(\displaystyle \angle COD=30^{\circ}+30^{\circ}=60^{\circ}{\small.}\)
Меньший угол между диагоналями данного прямоугольника равен \(\displaystyle 60^{\circ}{\small.}\)
Ответ: \(\displaystyle 60^{\circ}{\small.}\)
