В прямоугольнике \(\displaystyle ABCD\) \(\displaystyle \angle ABD=49^{\circ}{\small.}\) Найдите угол \(\displaystyle DCA{\small.}\)
\(\displaystyle ^{\circ}{\small.}\)
| Прямоугольником называется параллелограмм, у которого все углы прямые. |  |
\(\displaystyle ABCD\) – прямоугольник. \(\displaystyle \angle ABD=49^{\circ}{\small.}\)
Требуется найти угол \(\displaystyle DCA{\small.}\) | 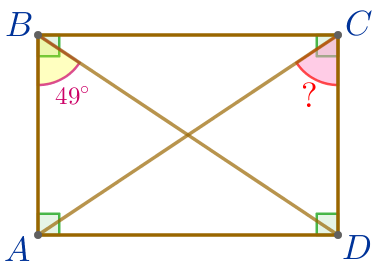 |
Рассмотрим треугольники \(\displaystyle BAD\) и \(\displaystyle CDA{\small.}\)
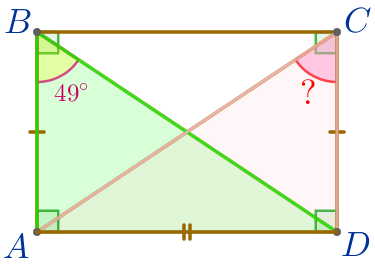 |
|
Следовательно,
\(\displaystyle \triangle BAD=\triangle CDA\) (по двум катетам)
В равных треугольниках соответственные углы равны, значит
\(\displaystyle \angle DCA=\angle ABD=49^{\circ}{\small.}\)
Ответ: \(\displaystyle 49^{\circ}{\small.}\)