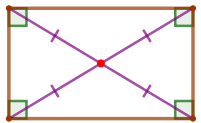
Диагонали \(\displaystyle AC\) и \(\displaystyle BD\) прямоугольника \(\displaystyle ABCD\) пересекаются в точке \(\displaystyle O{\small,}\) \(\displaystyle \angle BAO=55^{\circ}{\small.}\) Найдите угол \(\displaystyle AOB{\small.}\)
\(\displaystyle ^{\circ}{\small.}\)
\(\displaystyle O\) – точка пересечения диагоналей; \(\displaystyle \angle BAO=55^{\circ}{\small.}\)
Требуется найти угол \(\displaystyle AOB{\small.}\) | 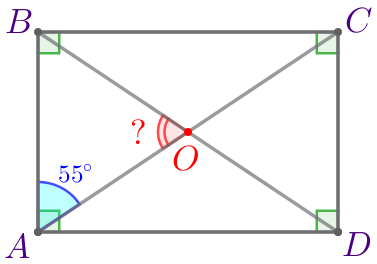 |
Рассмотрим треугольник \(\displaystyle AOB{\small.}\)
\(\displaystyle OA=OB{\small.}\)
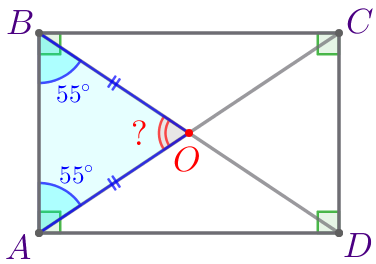 | Значит, \(\displaystyle \triangle AOB\) – равнобедренный. В равнобедренном треугольнике углы при основании равны. Следовательно, \(\displaystyle \angle BAO=\angle ABO=55^{\circ}{\small.}\) |
Сумма внутренних углов треугольника равна \(\displaystyle 180^{\circ}{\small.}\) Тогда
\(\displaystyle \angle AOB=180^{\circ}-(\angle BAO+\angle ABO)=180^{\circ}-(55^{\circ}+55^{\circ})=180^{\circ}-110^{\circ}=70^{\circ}{\small.}\)
Ответ: \(\displaystyle 70^{\circ}{\small.}\)