Определите, какие из точек \(\displaystyle M_1\left( \frac{1}{2};\frac{\sqrt3}{2}\right) \small,\) \(\displaystyle M_2\left( -\frac{9}{41};\frac{40}{41}\right) \small,\) \(\displaystyle M_3\left( \frac{1}{2};\frac{1}{2}\right) \small,\) \(\displaystyle M_4\left( -\frac{1}{2};\frac{\sqrt3}{2}\right) \)лежат на единичной окружности с центром в точке \(\displaystyle (0;\,0)\small.\)
| Лежат на единичной окружности | Не лежат на единичной окружности |
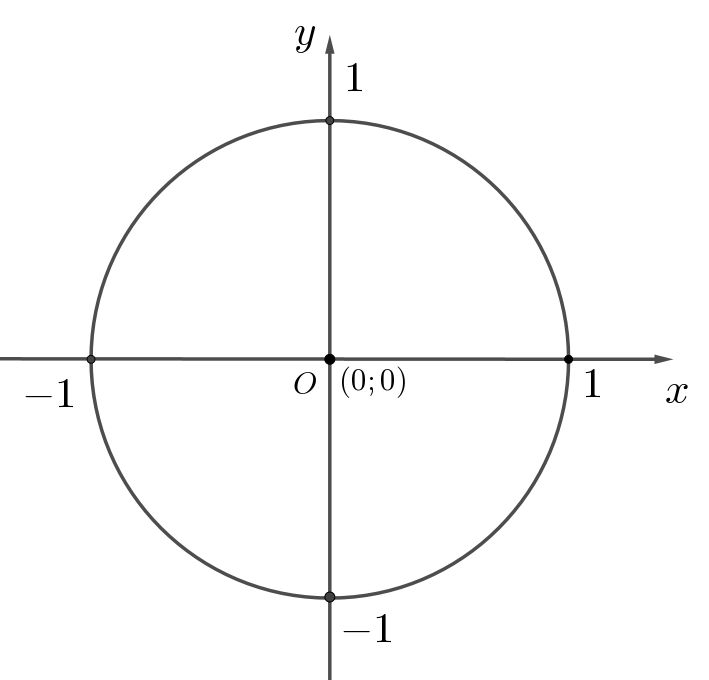
Единичная окружность с центром в точке \(\displaystyle (0;\,0)\) – это точки, находящиеся на расстоянии \(\displaystyle 1\) от точки \(\displaystyle (0;\,0)\small.\)
Тогда найдем расстояние от \(\displaystyle (0;\,0)\) до каждой из точек.
То есть \(\displaystyle M_1\) лежит на единичной окружности с центром в \(\displaystyle (0;\,0)\small.\)
Опустим из \(\displaystyle M_1\) перпендикуляр на ось \(\displaystyle Ox{\small:}\)
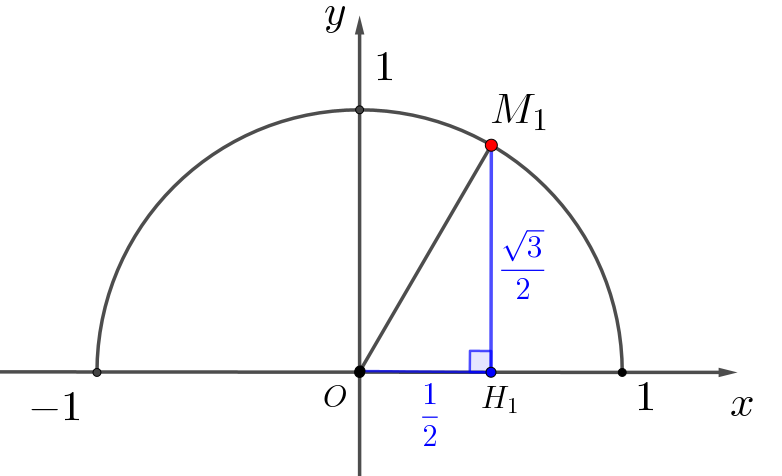
Получился прямоугольный треугольник с катетами \(\displaystyle \frac{1}{2}\) и \(\displaystyle \frac{\sqrt3}{2}\small.\)
Тогда по теореме Пифагора квадрат его гипотенузы равен сумме квадратов катетов:
\(\displaystyle OM_1^2=OH_1^2+M_1H_1^2=\left(\frac{1}{2}\right)^2+\left(\frac{\sqrt{3}}{2}\right)^2=\frac{1}{4}+\frac{3}{4}=1\small.\)
То есть
\(\displaystyle OM_1=\sqrt{1}=1\small.\)
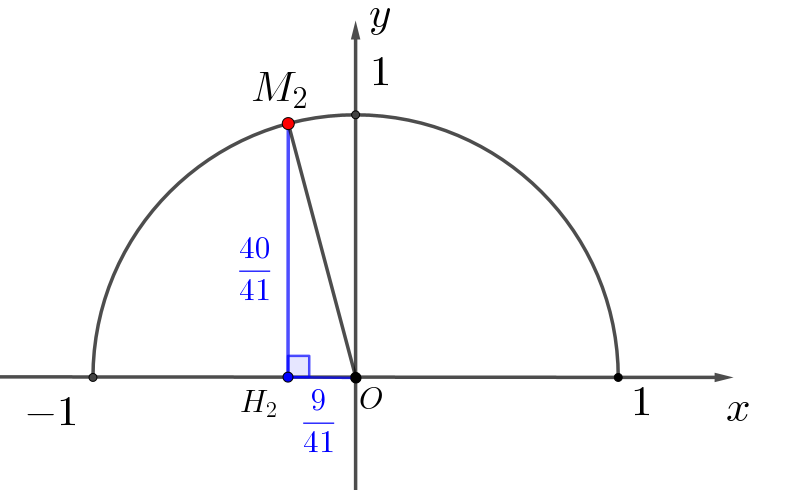
То есть \(\displaystyle M_2\) лежит на единичной окружности с центром в \(\displaystyle (0;\,0)\small.\)
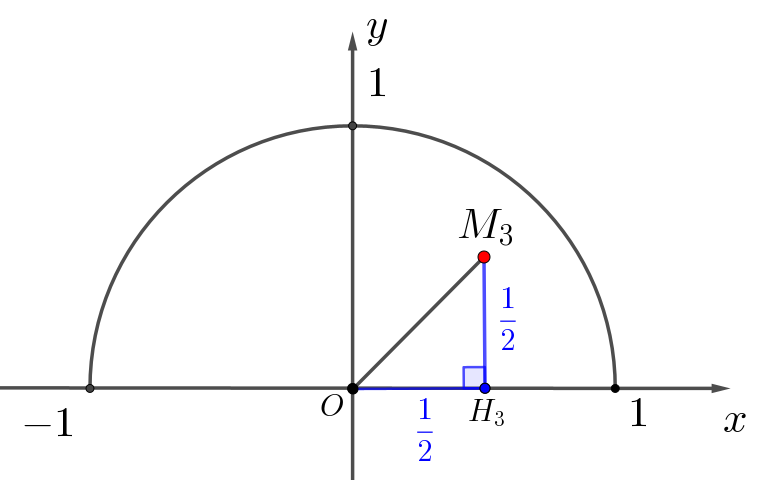
То есть \(\displaystyle M_3\) не лежит на единичной окружности с центром в \(\displaystyle (0;\,0)\small.\)
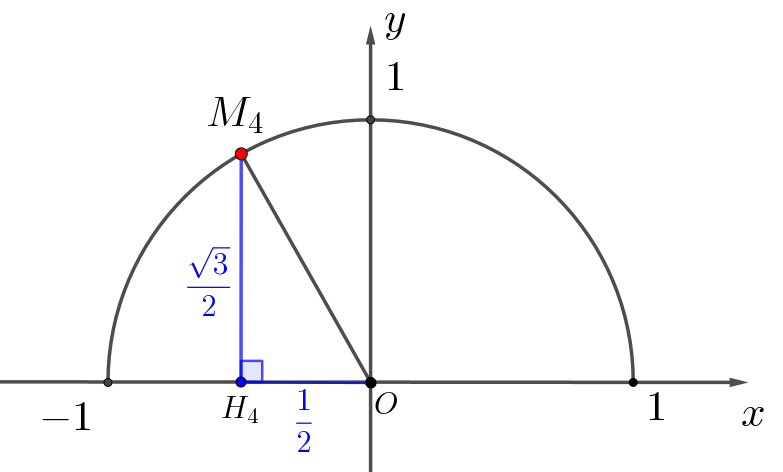
То есть \(\displaystyle M_4\) лежит на единичной окружности с центром в \(\displaystyle (0;\,0)\small.\)
Ответ:
| Лежат на единичной окружности | Не лежат на единичной окружности |
| \(\displaystyle M_1,\,M_2,\,M_4\) | \(\displaystyle M_3\) |