Точка \(\displaystyle M\) лежит на единичной полуокружности, ее координаты соответственно равны \(\displaystyle (\cos\color{red}\alpha,\,\sin\color{red}\alpha){\small:}\)
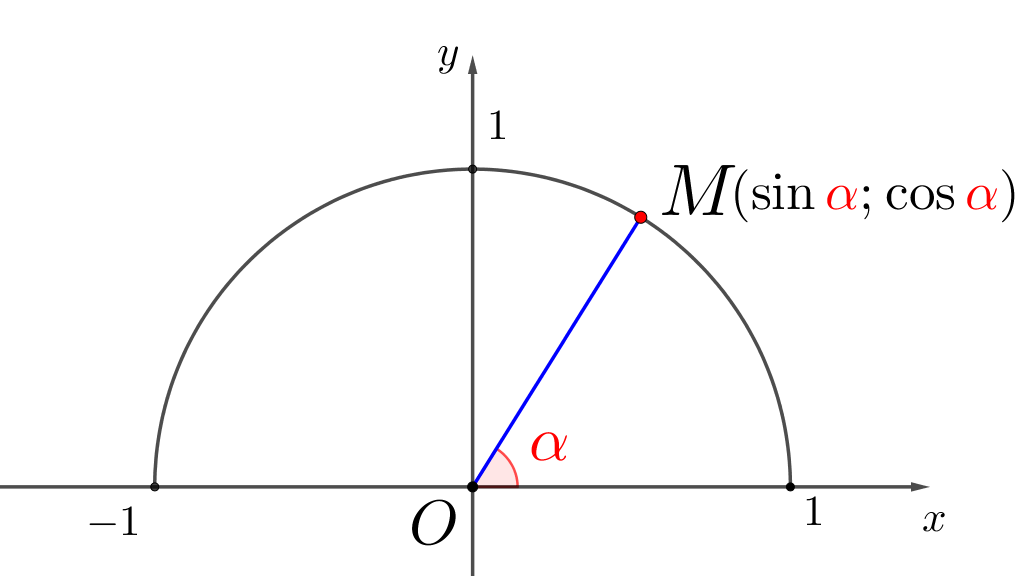
Найдите, чему равно:
\(\displaystyle \cos^2\color{red}\alpha+\sin^2\color{red}\alpha=\)
Опустим перпендикуляр из точки \(\displaystyle M\) на ось \(\displaystyle Ox\) и рассмотрим прямоугольный треугольник \(\displaystyle OMA\small{:}\)
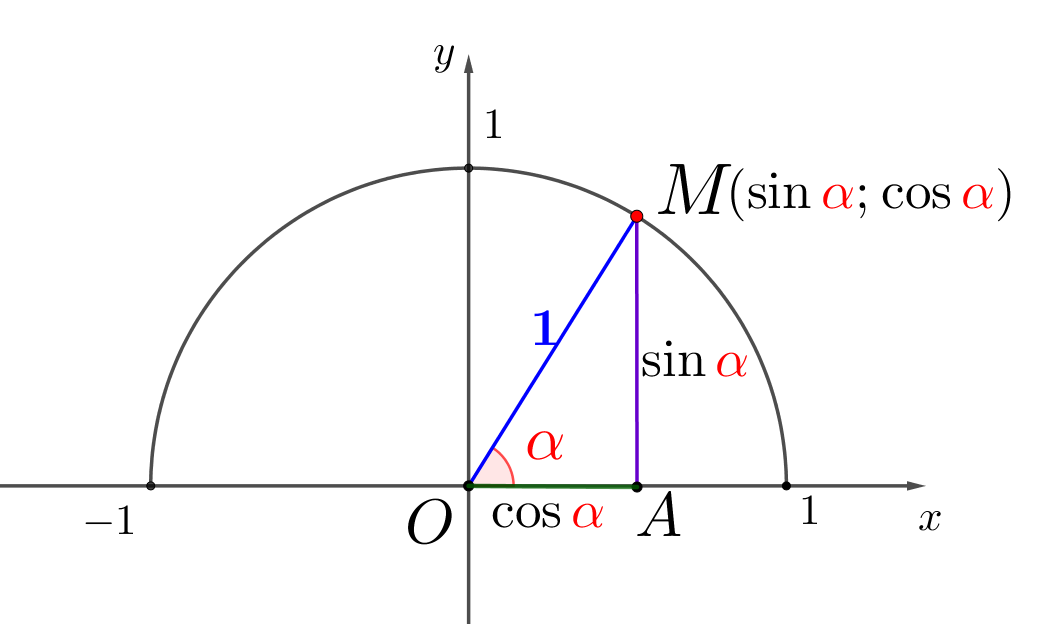
В этом треугольнике гипотенуза \(\displaystyle OM=1\small,\) катет \(\displaystyle OA=\cos{\color{red}\alpha}\) и катет \(\displaystyle MA=\sin{\color{red}\alpha}\small.\) Запишем теорему Пифагора для треугольника \(\displaystyle OMA\small{:}\)
\(\displaystyle OA^2+MA^2=OM^2\small.\)
Подставляя значения длин сторон, получаем
\(\displaystyle \cos^2\color{red}\alpha+\sin^2\color{red}\alpha=1\small.\)
Ответ: \(\displaystyle 1\small.\)