На рисунке треугольники, равенство которых доказывается по первому признаку.
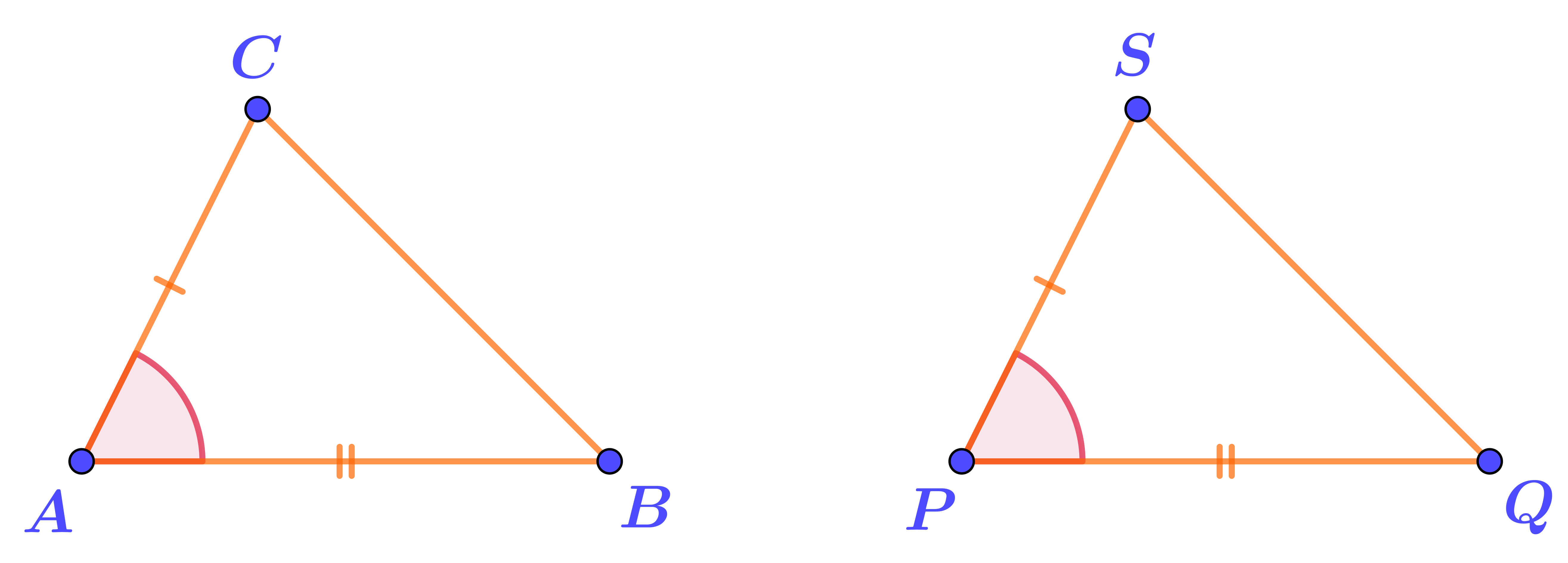
Заполните пропуски в доказательстве.
\(\displaystyle \begin{cases}\\\\\\\\\\\\\end{cases} \) | \(\displaystyle AB= PQ\) | \(\displaystyle {\LARGE\Rightarrow}\) |
|
| \(\displaystyle {\bf\angle}BAC = {\bf\angle}QPS\) | (по первому признаку) |
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.
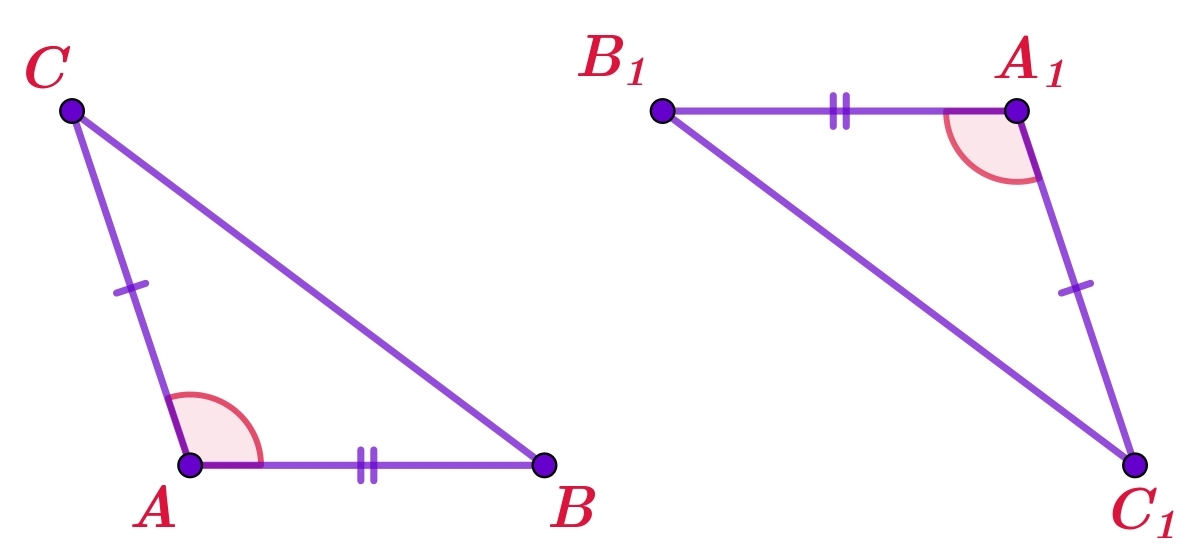
\(\displaystyle\left\{\begin{array}{}AB=A_1B_1\\AC=A_1C_1\\\angle BAC=\angle B_1A_1C_1\end{array} {\LARGE\Rightarrow} \quad {\bf\triangle}ABC={\bf\triangle}A_1B_1C_1\right.\)
Находим равные элементы треугольников и перечисляем в левой части выражения следствия.
В правую помещаем вывод о равенстве треугольников:
\(\displaystyle \begin{cases}\\\\\\\\\\\\\end{cases} \) | \(\displaystyle AB= PQ\) | \(\displaystyle {\LARGE\Rightarrow}\) |
|
| \(\displaystyle {\color{green}{AC= PS}}\) | \(\displaystyle {\color{green}{{\triangle}ABC={\triangle}PQS}}\) | ||
| \(\displaystyle {\bf\angle}BAC = {\bf\angle}QPS\) | (по первому признаку) |
Ответ: пропущенные выражения \(\displaystyle -\) \(\displaystyle AC= PS \) и \(\displaystyle {\triangle}ABC={\triangle}PQS {\small .}\)