На сторонах угла \(\displaystyle QPT\) отметили точки \(\displaystyle S\) и \(\displaystyle R{\small .}\)
При этом образовались отмеченные на рисунке равные отрезки.
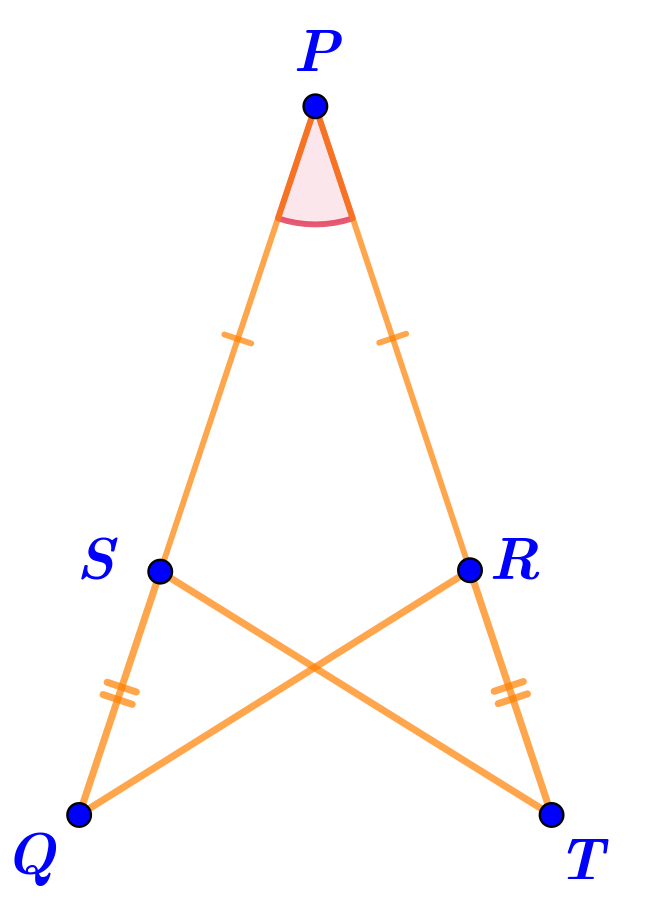
Заполните пропуски в доказательстве равенства треугольников \(\displaystyle PTS\) и \(\displaystyle PQR{\small .}\)
\(\displaystyle \begin{cases}\\\\\\\\\\\\\end{cases} \) | \(\displaystyle PS= PR\) | \(\displaystyle {\LARGE\Rightarrow}\) |
|
\(\displaystyle {\bf\triangle}PTS={\bf\triangle}PQR\) | |||
| (по первому признаку) |
По условию
\(\displaystyle PS=PR\) и \(\displaystyle SQ=RT{\small .}\)
Тогда
\(\displaystyle PQ=PS+SQ=PR+RT=PT{\small .}\)
В данных треугольниках
\(\displaystyle \begin{cases}\\\\\\\\\\\\\end{cases} \) | \(\displaystyle PS=PR\) | \(\displaystyle {\LARGE\Rightarrow}\) |
|
\(\displaystyle {\color{green}{PT=PQ}}\) | \(\displaystyle {\triangle}PTS={\triangle}PQR\) | ||
| \(\displaystyle {\color{green}{{\bf\angle}QPT-\footnotesize {общий\,угол}}}\) | (по первому признаку) |
Ответ: пропущенные выражения \(\displaystyle -\) \(\displaystyle PT=PQ{\small ,}\)\(\displaystyle {\bf\angle}QPT-\footnotesize {общий\,угол}{\small .}\)