Skip to main content

Теория: Определение параллелограмма по признакам

Задание

В четырёхугольнике \(\displaystyle ABCD\)  \(\displaystyle AB=17{\small,}\) \(\displaystyle BC=19{\small,}\) \(\displaystyle CD=17{\small,}\) \(\displaystyle AD=19{\small.}\)

Является ли четырёхугольник \(\displaystyle ABCD\) параллелограммом? 

Почему? 

Решение

Правило

Признак параллелограмма

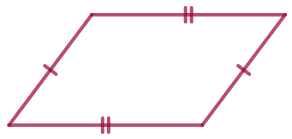Если у четырёхугольника противоположные стороны попарно равны,

то он является параллелограммом.

В четырёхугольнике \(\displaystyle ABCD{\small:}\)

  • \(\displaystyle AB=17{\small,}\) \(\displaystyle CD=17{\small,}\)
  • \(\displaystyle BC=19{\small,}\) \(\displaystyle AD=19{\small.}\)

То есть противоположные стороны попарно равны:

\(\displaystyle AB=CD{\small,}\)

\(\displaystyle BC=AD{\small.}\)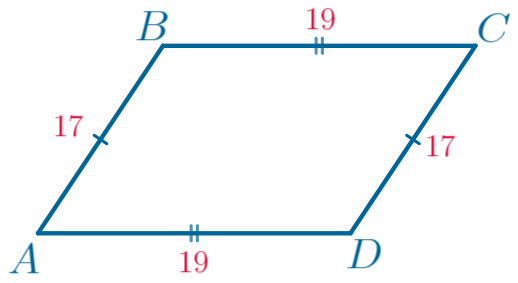

Значит, четырёхугольник \(\displaystyle ABCD\) является параллелограммом.

 

Ответ:

Является ли четырёхугольник \(\displaystyle ABCD\) параллелограммом?   Да.

Почему?   Противоположные стороны попарно равны.